【题目】如图所示，在四棱锥中，底面ABCD为直角梯形，，，，点E为AD的中点，，平面ABCD，且

（1）求证：；

（2）线段PC上是否存在一点F，使二面角的余弦值是？若存在，请找出点F的位置；若不存在，请说明理由．

（1）求证：MN//平面BCD；

（2）若AB=1，BC=，求直线AC与平面BCD所成的角.

【题目】如图，已知圆与轴的左右交点分别为，与轴正半轴的交点为.

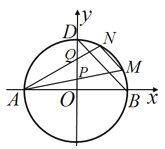
（1）若直线过点并且与圆相切，求直线的方程；

（2）若点是圆上第一象限内的点，直线分别与轴交于点，点是线段的中点，直线，求直线的斜率.

（1）证明：A1O⊥平面ABC；

（2）求直线AB与平面A1BC1所成角的正弦值．

①平面内与定点A（-3，0）和B（3，0）的距离之差等于4的点的轨迹为；

②点P是抛物线上的动点，点P在y轴上的射影是M点A的坐标是A（3，6），则的最小值是6；

③平面内到两定点距离之比等于常数的点的轨迹是圆；

④若过点C（1，1）的直线交椭圆于不同的两点A，B，且C是AB的中点，则直线的方程是．

⑤已知P为抛物线上一个动点，Q为圆上一个动点，那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是

其中真命题的序号是______．（写出所有真命题的序号）

（Ⅰ）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？

（Ⅱ）在（Ⅰ）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有一名男生的概率．

【题目】从2017年1月18日开始，支付宝用户可以通过“扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡（爱国福、富强福、和谐福、友善福，敬业福），除夕夜22:18，每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生，就除夕夜22：18之前是否集齐五福进行了一次调查（若未参与集五福的活动，则也等同于未集齐五福），得到具体数据如下表：

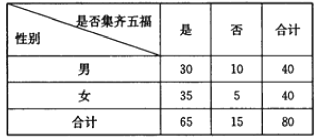
（1）根据如上的列联表，能否在犯错误的概率不超过0.05的前提下，认为“集齐五福与性别有关”？

（2）计算这80位大学生集齐五福的频率，并据此估算该校10000名在读大学生中集齐五福的人数；

（3）为了解集齐五福的大学生明年是否愿意继续参加集五福活动，该大学的学生会从集齐五福的学生中，选取2位男生和3位女生逐个进行采访，最后再随机选取3次采访记录放到该大学的官方网站上，求最后被选取的3次采访对象中至少有一位男生的概率.

参考公式： .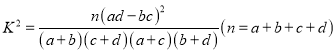

附表：

据此估计，该运动员四次投篮恰有两次命中的概率为____．

A. 若“”为假命题，则p，q均为假命题

B. “ ”是“”的充分不必要条件

C. “”的必要不充分条件是“”

D. 若命题p：，，则命题：，

【题目】已知为正的常数，函数.

（1）若，求函数的单调递增区间；

（2）设，求在区间上的最小值.（为自然对数的底数）