
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其离心率为
,其离心率为![]() ,以原点为圆心,椭圆的短轴长为直径的圆被直线
,以原点为圆心,椭圆的短轴长为直径的圆被直线![]() 截得的弦长等于
截得的弦长等于![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,过点
的左顶点,过点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过原点与
,过原点与![]() 平行的直线与椭圆相交于
平行的直线与椭圆相交于![]() 两点,问是否存在常数
两点,问是否存在常数![]() ,使
,使![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高二年级组织成语听说大赛,每班选10名同学参赛,要求每位同学回答5个成语,各位同学的得分总和算作本班成绩,其中一班的张明同学参赛,他每道题答对的概率均为![]() ,且每道题答对与否互不影响.计分办法规定为答对不超过3个题时,每答对一个得一分,超过三个,每多答对一个得两分.
,且每道题答对与否互不影响.计分办法规定为答对不超过3个题时,每答对一个得一分,超过三个,每多答对一个得两分.
(1)求张明至少答对三道题的概率;
(2)设张明答完5道题得分为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 满足下列3个条件:①函数
满足下列3个条件:①函数![]() 的图象过坐标原点; ②函数
的图象过坐标原点; ②函数![]() 的对称轴方程为
的对称轴方程为![]() ; ③方程
; ③方程![]() 有两个相等的实数根.
有两个相等的实数根.
(1)求函数![]() 的解析式;
的解析式;
(2)令![]() ,若函数
,若函数![]() 在
在![]() 上的最小值为-3,求实数
上的最小值为-3,求实数![]() 的值;
的值;
(3)令![]() ,若函数
,若函数![]() 在
在![]() 内有零点,求实数
内有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若方程![]() 两个根之和为4,两根之积为3,且过点(2,-1).求
两个根之和为4,两根之积为3,且过点(2,-1).求![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(ⅰ)求解关于![]() 的不等式
的不等式![]()
(ⅱ)设函数![]() ,求函数
,求函数![]() 的最大值
的最大值
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解高一学生暑假里在家读书情况,特随机调查了50名男生和50名女生平均每天的阅读时间(单位:分钟),统计如下表:

(1)根据统计表判断男生和女生谁的平均读书时间更长?并说明理由;
(2)求100名学生每天读书时间的平均数,并将每天平均时间超过和不超过平均数的人数填入下列的列联表:

(3)根据(2)中列联表,能否有99%的把握认为“平均阅读时间超过或不超过平均数是否与性别有关?”
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 是定义R的奇函数,当
是定义R的奇函数,当![]() 时,
时,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)画出函数![]() 的简图(不需要作图步骤),并求其单调递增区间
的简图(不需要作图步骤),并求其单调递增区间
(3)当![]() 时,求关于m的不等式
时,求关于m的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列几个命题:①若方程![]() 的两个根异号,则实数
的两个根异号,则实数![]() ;②函数
;②函数![]() 是偶函数,但不是奇函数;③函数
是偶函数,但不是奇函数;③函数 ![]() 在
在![]() 上是减函数,则实数a的取值范围是
上是减函数,则实数a的取值范围是![]() ;④ 方程
;④ 方程 ![]() 的根
的根![]() 满足
满足![]() ,则m满足的范围
,则m满足的范围![]() ,其中不正确的是( )
,其中不正确的是( )
A.①B.②C.③D.④
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.
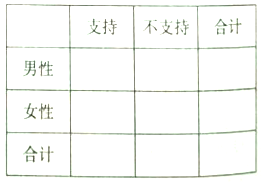
(Ⅰ)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附: 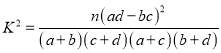 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com