
科目: 来源: 题型:
【题目】(题文)已知等差数列{an}的首项a1≠0,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4.
(1)求证:数列{bn}中的每一项都是数列{an}中的项;
(2)若a1=2,设cn=![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)在(2)的条件下,若有f(n)=log3Tn,求f(1)+f(2)+…+f(n)的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为保障公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,如图,检查员抽查某市一考点![]() ,以考点
,以考点![]() 正西
正西![]() 千米的
千米的![]() 处开始为检查起点,沿着一条北偏东
处开始为检查起点,沿着一条北偏东![]() 方向的公路
方向的公路![]() ,以每小时12千米的速度行驶,并用手机接通电话,问从起点开始计时,最长经过多少分钟检查员开始收不到信号(
,以每小时12千米的速度行驶,并用手机接通电话,问从起点开始计时,最长经过多少分钟检查员开始收不到信号(![]() 点开始),并至少持续多长时间(
点开始),并至少持续多长时间(![]() 之间)该考点才算检查合格?
之间)该考点才算检查合格?

查看答案和解析>>
科目: 来源: 题型:
【题目】下图是改革开放四十周年大型展览的展馆--------国家博物馆.现欲测量博物馆正门柱楼顶部一点![]() 离地面的高度
离地面的高度![]() (点
(点![]() 在柱楼底部).在地面上的两点
在柱楼底部).在地面上的两点![]() ,
,![]() 测得点
测得点![]() 的仰角分别为
的仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 米,则
米,则![]() 为( )
为( )

A. 10米 B. 20米 C. 30米 D. 40米
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)四边形![]() 的顶点在曲线
的顶点在曲线![]() 上,且对角线
上,且对角线![]() 均过坐标原点,若
均过坐标原点,若![]() .
.
(i) 求![]() 的范围;(ii) 求四边形
的范围;(ii) 求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
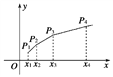
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P(x2,2),…,Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
(1)求数列{an}的通项公式;
(2){bn}为各项非零的等差数列,其前n项和为Sn.已知S2n+1=bnbn+1,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an} 和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 满足
满足![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求和: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据等差数列![]() 的
的![]() ,
, ![]() ,列出关于首项
,列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项![]() ,公比
,公比![]() 的方程组,解得
的方程组,解得![]() 、
、![]() 的值,求出数列
的值,求出数列![]() 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.
试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以![]() .
.
从而![]() .
.
【题型】解答题
【结束】
18
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的参数方程是
的参数方程是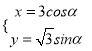 (
(![]() 为参数)以原点为极点,
为参数)以原点为极点, ![]() 轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线
轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 和
和![]() 上的任意点,求
上的任意点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com