【题目】等差数列的公差不为0，是其前项和，给出下列命题：

①若，且，则和都是中的最大项；

②给定，对一切，都有；

③若，则中一定有最小项；

④存在，使得和同号.

其中正确命题的个数为（ ）

A.4B.3C.2D.1

【题目】在锐角中，角的对边分别为，.

（1）求角的大小；

（2）若，求的取值范围.

【题目】已知椭圆的离心率，分别是椭圆的左、右焦点，过的直线与相交于A，B两点，的周长为。

(1)求椭圆的方程；

(2)是否存在直线使为直角，若存在求出此时直线的方程；若不存在，请说明理由。

【题目】2021年我省将实施新高考，新高考“依据统一高考成绩、高中学业水平考试成绩，参考高中学生综合素质评价信息”进行人才选拔。我校2018级高一年级一个学习兴趣小组进行社会实践活动，决定对某商场销售的商品A进行市场销售量调研，通过对该商品一个阶段的调研得知，发现该商品每日的销售量（单位：百件）与销售价格（元/件）近似满足关系式，其中为常数已知销售价格为3元/件时，每日可售出该商品10百件。

(1)求函数的解析式；

(2)若该商品A的成本为2元/件，根据调研结果请你试确定该商品销售价格的值，使该商场每日销售该商品所获得的利润（单位：百元）最大。

【题目】(理)某电视台举办的闯关节目共有五关，只有通过五关才能获得奖金，规定前三关若有失败即结束，后两关若有失败再给一次从失败的关开始继续向前闯的机会(后两关总共只有一次机会)，已知某人前三关每关通过的概率都是，后两关每关通过的概率都是.

(1)求该人获得奖金的概率；

(2)设该人通过的关数为X，求随机变量X的分布列及数学期望．

【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:

以最高气温位于各区间的频率代替最高气温位于该区间的概率.

(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.

(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?

【题目】已知a，b，c分别是△ABC的内角A，B，C的对边，若△ABC的周长为2(＋1)，且sin B＋sin C＝sin A，则a＝ (　　)

A. B. 2 C. 4 D.

【答案】B

【解析】

根据正弦定理把转化为边的关系，进而根据△ABC的周长，联立方程组，可求出a的值．

根据正弦定理，可化为

∵△ABC的周长为，

∴联立方程组，

解得a=2．

故选：B

【点睛】

（1）在三角形中根据已知条件求未知的边或角时，要灵活选择正弦、余弦定理进行边角之间的转化，以达到求解的目的．

（2）求角的大小时，在得到角的某一个三角函数值后，还要根据角的范围才能确定角的大小，这点容易被忽视，解题时要注意．

【题型】单选题
【结束】
7

A. (－∞，2] B. (－∞，2) C. (－∞，3] D. (－∞，3)

【题目】在海岸处，发现北偏东方向，距离为海里的处有一艘走私船，在处北偏西方向，距离为海里的处有一艘缉私艇奉命以海里/时的速度追截走私船，此时，走私船正以海里/时的速度从处向北偏东方向逃窜.

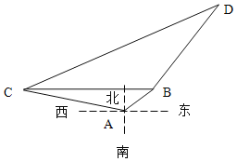
（1）问船与船相距多少海里？船在船的什么方向？

（2）问缉私艇沿什么方向行驶才能最快追上走私船？并求出所需时间.

【题目】已知时，函数有极值

（1）求实数的值；

（2）若方程有3个实数根，求实数的取值范围。

【题目】甲、乙两支球队进行总决赛，比赛采用七场四胜制，即若有一队先胜四场，则此队为总冠军，比赛就此结束.因两队实力相当，每场比赛两队获胜的可能性均为.据以往资料统计，第一场比赛可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元.

(I)求总决赛中获得门票总收入恰好为300万元的概率；

(II)设总决赛中获得门票总收入为X，求X的均值E(X).