
科目: 来源: 题型:
【题目】如图为两种商品2019年前三季度销售量的折线统计图,结合统计图,下列说法中正确的有________.
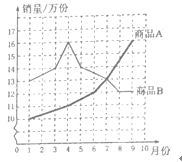
①1~6月,商品![]() 的月销售量都超过商品
的月销售量都超过商品![]()
②7月份商品![]() 与商品
与商品![]() 的销售量相等
的销售量相等
③对于商品![]() ,7~8月的月销售量增长率与8~9月的月销售量增长率相同
,7~8月的月销售量增长率与8~9月的月销售量增长率相同
④2019年前三季度商品![]() 的销量逐月增长
的销量逐月增长
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三年级有1000人,某次数学考试不同成绩段的人数![]() .
.
(1)求该校此次数学考试平均成绩;
(2)计算得分超过141的人数;
(3)甲同学每次数学考试进入年级前100名的概率是![]() ,若本学期有4次考试,
,若本学期有4次考试, ![]() 表示进入前100名的次数,写出
表示进入前100名的次数,写出![]() 的分布列,并求期望与方差.
的分布列,并求期望与方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆方程为![]() ,离心率为
,离心率为![]() ,
, ![]() 是椭圆的两个焦点,
是椭圆的两个焦点, ![]() 为椭圆上一点且
为椭圆上一点且![]() ,
, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆的方程;
(2)已知点![]() ,直线
,直线![]() 不经过点
不经过点![]() 且与椭圆交于
且与椭圆交于![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之和为1,证明直线
的斜率之和为1,证明直线![]() 过定点,并求出该定点.
过定点,并求出该定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正四棱锥![]() 中,底边
中,底边![]() ,侧棱
,侧棱![]() ,
, ![]() 为侧棱
为侧棱![]() 上的点.
上的点.
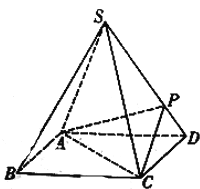
(1)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值的大小;
的余弦值的大小;
(2)若![]() ,侧棱
,侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(一)在函数图象的学习中常常用到化归转化的思想,往往通过对一些已经学习过的函数图象的研究,进一步迁移到其它函数,例如函数![]() 与正弦函数就有密切的联系,因为
与正弦函数就有密切的联系,因为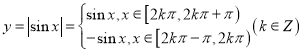 .只需将
.只需将![]() 在
在![]() 轴下方的图象翻折到上方,就得到
轴下方的图象翻折到上方,就得到![]() 的图象.
的图象.
(二)在研究函数零点问题时,往往会将函数零点问题转化为两个函数图象的交点问题.例如研究函数![]() 的零点就可以转化为函数
的零点就可以转化为函数![]() 与函数
与函数![]() 的图象交点来进行处理,通过作图不仅知道函数
的图象交点来进行处理,通过作图不仅知道函数![]() 有且仅有一个零点,还可以确定零点
有且仅有一个零点,还可以确定零点![]() .这体现了化归转化与数形结合的思想在函数研究中的应用.
.这体现了化归转化与数形结合的思想在函数研究中的应用.
结合阅读材料回答下面两个问题:
![]() 作出函数
作出函数![]() 的图象;
的图象;
![]() 利用作图的方法验证函数
利用作图的方法验证函数![]() 有且仅有两个零点.若记两个零点分别为
有且仅有两个零点.若记两个零点分别为![]() ,
,![]() ,证明:
,证明:![]() .(注:在同一坐标中作图)
.(注:在同一坐标中作图)
查看答案和解析>>
科目: 来源: 题型:
【题目】某营养协会对全市18岁男生的身高作调查,统计显示全市18岁男生的身高服从正态分布![]() ,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于
,现某校随机抽取了100名18岁男生的身高分析,结果这100名学生的身高全部介于![]() 到
到![]() 之间.现将结果按如下方式分为6组,第一组
之间.现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
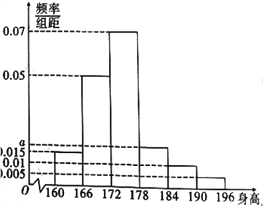
(1)若全市18岁男生共有![]() 人,试估计该市身高在
人,试估计该市身高在![]() 以上的18岁男生人数;
以上的18岁男生人数;
(2)求![]() 的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
的值,并计算该校18岁男生的身高的中位数(精确到小数点后三位);
(3)若身高![]() 以上的学生校服需要单独定制,现从这100名学生中身高在
以上的学生校服需要单独定制,现从这100名学生中身高在![]() 以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为
以上的同学中任意抽取3人,这三人中校服需要单独定制的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: ![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 满足如下条件:
满足如下条件:
①函数![]() 的最小值为
的最小值为![]() ,最大值为9;
,最大值为9;
②![]() 且
且![]() ;
;
③若函数![]() 在区间
在区间![]() 上是单调函数,则
上是单调函数,则![]() 的最大值为2.
的最大值为2.
试探究并解决如下问题:
(Ⅰ)求![]() ,并求
,并求![]() 的值;
的值;
(Ⅱ)求函数![]() 的图象的对称轴方程;
的图象的对称轴方程;
(Ⅲ)设![]() 是函数
是函数![]() 的零点,求
的零点,求![]() 的值的集合.
的值的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com