据此估计，该运动员三次投篮恰有两次命中的概率为

A. B. C. D.

（1）若k=-5，求f（x）的极值；

（2）若f（x）在区间（0，3）内单调，求实数k的取值范围．

【题目】已知函数是偶函数，且满足，当时， ，当时， 的最大值为.

（1）求实数的值；

（2）函数，若对任意的，总存在，使不等式恒成立，求实数的取值范围.

【题目】已知椭圆C：+=1（a＞b＞0）经过点（1，），且焦距为2．

（1）求椭圆C方程；

（2）椭圆C的左，右焦点分别为F1，F2，过点F2的直线l与椭圆C交于A，B两点，求△F2AB面积S的最大值并求出相应直线l的方程．

【题目】已知椭圆： 的离心率为，直线交椭圆于、两点，椭圆的右顶点为，且满足.

（1）求椭圆的方程；

（2）若直线与椭圆交于不同两点、，且定点满足，求实数的取值范围.

【题目】如图，四棱锥的底面是菱形，且，其对角线、交于点， 、是棱、上的中点.

（1）求证：面面；

（2）若面底面， ， ， ，求三棱锥的体积.

【题目】在三棱锥A﹣BCD中，BCD是边长为的等边三角形，，二面角A﹣BC﹣D的大小为θ，且，则三棱锥A﹣BCD体积的最大值为（ ）

A.B.C.D.

【题目】3月12日，全国政协总工会界别小组会议上，人社部副部长汤涛在回应委员呼声时表示无论是从养老金方面，还是从人力资源的合理配置来说，延迟退休是大势所趋.不过，汤部长也表示，不少职工对于延迟退休有着不同的意见.某高校一社团就是否同意延迟退休的情况随机采访了200名市民，并进行了统计，得到如下的列联表：

（1）根据上面的列联表判断能否有的把握认为对延迟退休的态度与性别有关；

（2）为了进一步征求对延迟退休的意见和建议，从抽取的200位市民中对不赞同的按照分层抽样的方法抽取6人，再从这6人中随机抽出3名进行电话回访，求3人中至少有1人为男性的概率.

附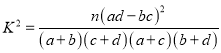： ，其中.

【题目】已知函数.

（1）求函数的单调区间；

（2）设函数， ， 为自然对数的底数.当时，若， ，不等式成立，求的最大值.