
科目: 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,则互为对立事件是( )
个球,则互为对立事件是( )
A. 至少有一个黒球与都是黒球B. 至少有一个黒球与都是红球
C. 至少有一个黒球与至少有![]() 个红球D. 恰有
个红球D. 恰有![]() 个黒球与恰有
个黒球与恰有![]() 个黒球
个黒球
查看答案和解析>>
科目: 来源: 题型:
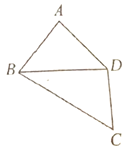
【题目】如图所示,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .将四边形
.将四边形![]() 沿对角线
沿对角线![]() 折成四面体
折成四面体![]() ,使平面
,使平面![]() 平面
平面![]() ,则下列结论中正确的结论个数是( )
,则下列结论中正确的结论个数是( )

①![]() ;②
;②![]() ;
;
③![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
④四面体![]() 的体积为
的体积为![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,半圆的直径![]() ,
,![]() 为圆心,
为圆心,![]() ,
,![]() 为半圆上的点.
为半圆上的点.

(Ⅰ)请你为![]() 点确定位置,使
点确定位置,使![]() 的周长最大,并说明理由;
的周长最大,并说明理由;
(Ⅱ)已知![]() ,设
,设![]() ,当
,当![]() 为何值时,
为何值时,
(ⅰ)四边形![]() 的周长最大,最大值是多少?
的周长最大,最大值是多少?
(ⅱ)四边形![]() 的面积最大,最大值是多少?
的面积最大,最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
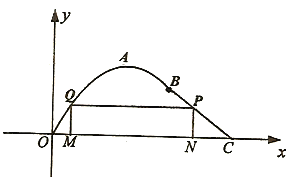
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com