
科目: 来源: 题型:
【题目】某校![]() 位同学的数学与英语成绩如下表所示:
位同学的数学与英语成绩如下表所示:
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
将这![]() 位同学的两科成绩绘制成散点图如下:
位同学的两科成绩绘制成散点图如下:
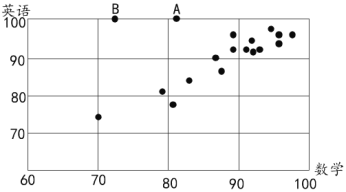
(1)根据该校以往的经验,数学成绩![]() 与英语成绩
与英语成绩![]() 线性相关.已知这
线性相关.已知这![]() 名学生的数学平均成绩为
名学生的数学平均成绩为![]() ,英语平均成绩为
,英语平均成绩为![]() .考试结束后学校经过调查发现学号为
.考试结束后学校经过调查发现学号为![]() 的
的![]() 同学与学号为
同学与学号为![]() 的
的![]() 同学(分别对应散点图中的
同学(分别对应散点图中的![]() 、
、![]() )在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
)在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
(2)取消两位作弊同学的两科成绩后,求数学成绩![]() 与英语成绩
与英语成绩![]() 的线性回归方程
的线性回归方程![]() ,并据此估计本次英语考试学号为
,并据此估计本次英语考试学号为![]() 的同学如果没有作弊的英语成绩(结果保留整数).
的同学如果没有作弊的英语成绩(结果保留整数).
附:![]() 位同学的两科成绩的参考数据:
位同学的两科成绩的参考数据:![]() ,
,![]() .
.
参考公式: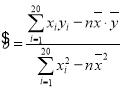 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足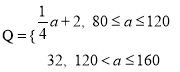 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆具有以下性质:设A,B是圆C:![]() 上关于原点对称的两点,点P是圆上的任意一点.若直线PA,PB的斜率都存在并分别记为
上关于原点对称的两点,点P是圆上的任意一点.若直线PA,PB的斜率都存在并分别记为![]() ,
,![]() ,则
,则![]() =﹣1,是与点P的位置无关的定值.
=﹣1,是与点P的位置无关的定值.
(1)试类比圆的上述性质,写出椭圆![]() 的一个类似性质,并加以证明;
的一个类似性质,并加以证明;
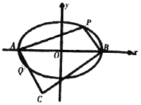
(2)如图,若椭圆M的标准方程为![]() ,点P在椭圆M上且位于第一象限,点A,B分别为椭圆长轴的两个端点,过点A,B分别作
,点P在椭圆M上且位于第一象限,点A,B分别为椭圆长轴的两个端点,过点A,B分别作![]() ⊥PA,
⊥PA,![]() ⊥PB,直线
⊥PB,直线![]() ,
,![]() 交于点C,直线
交于点C,直线![]() 与椭圆M的另一交点为Q,且
与椭圆M的另一交点为Q,且![]() ,求
,求![]() 的取值范围(可直接使用(1)中证明的结论).
的取值范围(可直接使用(1)中证明的结论).
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各对事件中,不互为相互独立事件的是( )
A.掷一枚骰子一次,事件![]() “出现偶数点”;事件
“出现偶数点”;事件![]() “出现3点或6点”
“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件![]() “第一次摸到白球”,事件
“第一次摸到白球”,事件![]() “第二次摸到白球”
“第二次摸到白球”
C.袋中有3白、2黑共5个大小相同的小球,依次不放回地摸两球,事件![]() “第一次摸到白球”,事件
“第一次摸到白球”,事件![]() “第二次摸到黑球”
“第二次摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件![]() “从甲组中选出1名男生”,事件
“从甲组中选出1名男生”,事件![]() “从乙组中选出1名女生”
“从乙组中选出1名女生”
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
参考公式:
查看答案和解析>>
科目: 来源: 题型:
【题目】某社区组织“学习强国”的知识竞赛,从参加竞赛的市民中抽出40人,将其成绩分成以下6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
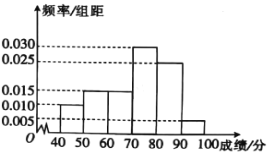
,第6组![]() ,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
A.1,3,4B.2,3,3C.2,2,4D.1,1,6
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个说法:
①命题“![]() ,都有
,都有![]() ”的否定是“
”的否定是“![]() ,使得
,使得![]() ”;
”;
②已知![]() 、
、![]() ,命题“若
,命题“若![]() ,则
,则![]() ”的逆否命题是真命题;
”的逆否命题是真命题;
③![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④若![]() 为函数
为函数![]() 的零点,则
的零点,则![]() .
.
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com