
科目: 来源: 题型:
【题目】已知函数![]()
(1)用“五点法”作出![]() 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图;
(2)写出![]() 的对称中心与单调递增区间,并求
的对称中心与单调递增区间,并求![]() 振幅、周期、频率、相位及初相;
振幅、周期、频率、相位及初相;
(3)求![]() 的最大值以及取得最大值时x的集合.
的最大值以及取得最大值时x的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面六个命题中,其中正确的命题序号为______________.
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() ,
,![]() 的单调递减区间为
的单调递减区间为![]() ;
;
⑤将函数![]() 向右平移
向右平移![]() (
(![]() )个单位所得图象关于
)个单位所得图象关于![]() 轴对称,则
轴对称,则![]() 的最小正值为
的最小正值为![]() ;
;
⑥关于![]() 的方程
的方程![]() 的两个实根中,一个根比1大,一个根比-1小,则
的两个实根中,一个根比1大,一个根比-1小,则![]() 的取值范围为
的取值范围为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】若数列![]() 对任意
对任意![]() 满足
满足![]() ,下面给出关于数列
,下面给出关于数列![]() 的四个命题:①
的四个命题:①![]() 可以是等差数列,②
可以是等差数列,②![]() 可以是等比数列;③
可以是等比数列;③![]() 可以既是等差又是等比数列;④
可以既是等差又是等比数列;④![]() 可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】若在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数有“和一点”
成立,则称函数有“和一点”![]() .
.
(1)函数![]() 是否有“和一点”?请说明理由;
是否有“和一点”?请说明理由;
(2)若函数![]() 有“和一点”,求实数
有“和一点”,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() 有“和一点”.
有“和一点”.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图半圆![]() 的直径为4,
的直径为4,![]() 为直径
为直径![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 为半圆周上任一点,以
为半圆周上任一点,以![]() 为边作等边
为边作等边![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列)
按顺时针方向排列)
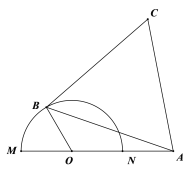
(1)若等边![]() 边长为
边长为![]() ,
,![]() ,试写出
,试写出![]() 关于
关于![]() 的函数关系;
的函数关系;
(2)问![]() 为多少时,四边形
为多少时,四边形![]() 的面积最大?这个最大面积为多少?
的面积最大?这个最大面积为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:

(1)已知该校有![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足![]() 小时的人数.
小时的人数.
(2)若从学习时间不少于![]() 小时的学生中选取
小时的学生中选取![]() 人,设选到的男生人数为
人,设选到的男生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
(3)试比较男生学习时间的方差![]() 与女生学习时间方差
与女生学习时间方差![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数为常数![]()
(1)当![]() 在
在![]() 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围.
上恰有两个不相等的实数根,求实数b的取值范围.
(2)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为![]() ,
, ![]() ,
, ![]() (
(![]() ,且
,且![]() ,
, ![]() ,
, ![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com