【题目】如图所示，某地出土的一种“钉”是由四条线段组成，其结构能使它任意抛至水平面后，总有一端所在的直线竖直向上．并记组成该“钉”的四条等长的线段公共点为，钉尖为．

（1）判断四面体的形状，并说明理由；

（2）设，当在同一水平面内时，求与平面所成角的大小（结果用反三角函数值表示）；

（3）若该“钉”着地后的四个线段根据需要可以调节与底面成角的大小，且保持三个线段与底面成角相同，若，，问为何值时，的体积最大，并求出最大值．

（Ⅰ）求证AE⊥平面BCE；

（Ⅱ）求二面角B—AC—E的余弦值.

【题目】就实数的取值范围，讨论关于的函数与 轴的交点个数.

【题目】在直角坐标系中曲线的参数方程为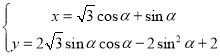（为参数）．若以直角坐标系中的原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

（1）求曲线的普通方程和曲线的直角坐标方程；

（2）若曲线与曲线有公共点，求实数的取值范围．

【题目】某化工厂一种溶液的成品，生产过程的最后工序是过滤溶液中的杂质，过滤初期溶液含杂质为2%，每经过一次过滤均可使溶液杂质含量减少，记过滤次数为x（）时溶液杂质含量为y.

（1）写出y与x的函数关系式；

（2）按市场要求，出厂成品杂质含量不能超过0.1%，问至少经过几次过滤才能使产品达到市场要求？（参考数据：，）

（1）依据上述数据，能否在犯错误的概率不超过的前提下认为该市市民进行网络购物的情况与性别有关？

（2）现从所抽取的女性网民中利用分层抽样的方法再抽取人，从这人中随机选出人赠送网络优惠券，求出选出的人中至少有两人是经常进行网络购物的概率；

（3）将频率视为概率，从该市所有的参与调查的网民中随机抽取人赠送礼物，记经常进行网络购物的人数为，求的期望和方差.

附：，其中

【题目】已知函数的图像与x轴相邻的两交点间的距离为，把函数的图像沿x轴向左平移个单位，得到函数的图像，关于函数，现有如下命题：

①在上是减函数；②其图像关于点对称；

③函数是奇函数；④当时，函数的值域为.

其中真命题的个数为（ ）

A.1B.2C.3D.4

【题目】已知椭圆的左右顶点分别是，，点在椭圆上，过该椭圆上任意一点P作轴，垂足为Q，点C在的延长线上，且．

（1）求椭圆的方程；

（2）求动点C的轨迹E的方程；

（3）设直线（C点不同A、B）与直线交于R，D为线段的中点，证明：直线与曲线E相切；

【题目】某校从参加高二年级期末考试的学生中抽出60名学生，并统计了他们的物理成绩（成绩均为整数且满分为100分），把其中不低于50分的分成五段，，……，后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：

（1）求出物理成绩低于50分的学生人数；

（2）估计这次考试物理学科及格率（60分以上为及格）；

（3）从物理成绩不及格的学生中选x人，其中恰有一位成绩不低于50分的概率为，求此时x的值；

【题目】在四棱锥中， 平面， ， ， ， .

（1）证明；

（2）求二面角的余弦值；

（3）设点为线段上一点，且直线平面所成角的正弦值为，求的值.