【题目】如图,椭圆：的左、右焦点分别为，椭圆上一点与两焦点构成的三角形的周长为6,离心率为，

（Ⅰ）求椭圆的方程；

（Ⅱ）过点的直线交椭圆于两点,问在轴上是否存在定点,使得为定值？证明你的结论.

【题目】定义在R上函数，若函数关于点对称，且则关于x的方程()有n个不同的实数解，则n的所有可能的值为( )

A.2B.4

C.2或4D.2或4或6

【题目】在平面直角坐标系中，点，点.已知抛物线(是常数)，顶点为.

(1)当抛物线经过点时，求顶点的坐标；

(2)若点在轴下方，当时，求抛物线的解析式；

(3)无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.

【题目】在平面直角坐标系中，四边形是矩形，点，点，点.以点为中心，顺时针旋转矩形，得到矩形，点的对应点分别为.

（1）如图①，当点落在边上时，求点的坐标；

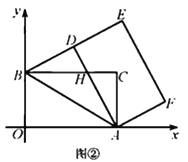
（2）如图②，当点落在线段上时，与交于点.

①求证；②求点的坐标.

（3）记为矩形对角线的交点，为的面积，求的取值范围(直接写出结果即可).

【题目】如图，点、，点是圆上一动点，线段的垂直平分线交线段于点，设点的轨迹为曲线.且直线交曲线于两点（点在轴的上方）.

（1）求曲线的方程；

（2）试判断直线与曲线的另一交点是否与点关于轴对称？

【题目】如图，是南北方向的一条公路，是北偏东方向的一条公路，某风景区的一段边界为曲线．为方便游客光，拟过曲线上的某点分别修建与公路，垂直的两条道路，，且，的造价分别为5万元百米，40万元百米，建立如图所示的直角坐标系，则曲线符合函数模型，设，修建两条道路，的总造价为万元，题中所涉及的长度单位均为百米．

（1）求解析式；

（2）当为多少时，总造价最低？并求出最低造价．

（1）若以“年龄45岁为分界点”，由以上统计数据完成下面的2×2列联表，并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”？

若从年龄在[55，65），[65，75）的别调查的人中各随机选取两人进行追踪调查，记选中的4人中赞成“使用微信交流”的人数为X，求随机变量X的分布列及数学期望．

参考数据：

参考公式：K2=，其中n=a+b+c+d．

【题目】某养鸡场有2500只鸡准备对外出售从中随机抽取了一部分鸡，根据它们的质量(单位:)，绘制出如下的统计图①和图②请根据相关信息，解答下列问题：

（1）图①中的值为___________；

（2）统计这组数据的平均数众数和中位数；

（3）根据样本数据，估计这2500只鸡中，质量为的约有多少只?

【题目】有一段“三段论”，其推理是这样的：对于可导函数，若，则是函数的极值点,因为函数满足，所以是函数的极值点”，结论以上推理　　

A. 大前提错误B. 小前提错误C. 推理形式错误D. 没有错误

【题目】已知抛物线(为常数，)经过点，其对称轴在轴右侧，有下列结论:①抛物线经过点；②方程有两个不相等的实数根；③.其中，正确结论的个数为( )

A.0B.1C.2D.3