
科目: 来源: 题型:
【题目】在竖直坐标平面![]() 中,从坐标原点
中,从坐标原点![]() 出发以同一初速度
出发以同一初速度![]() 和不同的发射角(即发射方向与
和不同的发射角(即发射方向与![]() 轴正向之间的夹角)
轴正向之间的夹角)![]() 射出的质点(不计质点的大小),在重力(设重力加速度为
射出的质点(不计质点的大小),在重力(设重力加速度为![]() )的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线
)的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线![]() 在其上的点
在其上的点![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学在研究函数![]() 时,给出下面几个结论:
时,给出下面几个结论:
①等式![]() 对
对![]() 恒成立;
恒成立;
②函数的值域为![]() ;
;
③若![]() ,则一定
,则一定![]() ;
;
④对任意的![]() ,若函数
,若函数![]() 恒成立,则当
恒成立,则当![]() 时,
时,![]() 或
或![]() .
.
其中正确的结论是____________(写出所有正确结论的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业加工生产一批珠宝,要求每件珠宝都按统一规格加工,每件珠宝的原材料成本为3.5万元,每件珠宝售价(万元)与加工时间![]() (单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间
(单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间![]() (天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
(天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
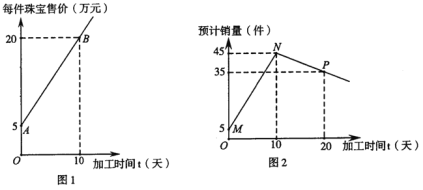
(1)如果每件珠宝加工天数分别为6,12,预计销量分别会有多少件?
(2)设工厂生产这批珠宝产生的纯利润为![]() (万元),请写出纯利润
(万元),请写出纯利润![]() (万元)关于加工时间
(万元)关于加工时间![]() (天)之间的函数关系式,并求纯利润
(天)之间的函数关系式,并求纯利润![]() (万元)最大时的预计销量.
(万元)最大时的预计销量.
注:毛利润=总销售额-原材料成本,纯利润=毛利润-工人报酬
查看答案和解析>>
科目: 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用![]() 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为![]() 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:厘米)满足关系:
(单位:厘米)满足关系:![]() .若不建隔热层,每年的能源消耗费用为
.若不建隔热层,每年的能源消耗费用为![]() 万元.设
万元.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 最小,并求其最小值.
最小,并求其最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,其中,角
,其中,角![]() 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与![]() 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点![]() ,且
,且![]() .
.
(Ⅰ)若![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若点![]() 为线性约束条件
为线性约束条件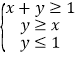 所围成的平面区域上的一个动点,试确定角
所围成的平面区域上的一个动点,试确定角![]() 的取值范围,并求函数
的取值范围,并求函数![]() 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题![]() :
:![]() ,
,![]() ,则命题
,则命题![]() :
:![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C. 命题“若![]() ,则
,则![]() 或
或![]() ”的逆否命题是“若
”的逆否命题是“若![]() 或
或![]() ,则
,则![]() ”
”
D. 命题![]() :
:![]() ,
,![]() ;命题
;命题![]() :对
:对![]() ,总有
,总有![]() ;则
;则![]() 是真命题
是真命题
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是规划的生态文旅园区,其中
区域(含边界)是规划的生态文旅园区,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为
、半径为![]() 千米.根据发展规划,要在扇形
千米.根据发展规划,要在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
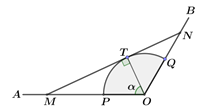
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数;
的函数;
(2)已知公路每千米的造价为![]() 万元,问建造这样一条公路
万元,问建造这样一条公路![]() ,至少要投入多少万元?
,至少要投入多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com