甲：132，108，112，121，113，121，118，128，118，129；

乙：133，107，120，113，122，114，128，118，129，127.

(1)画出甲、乙两班学生数学成绩的茎叶图，并根据茎叶图判断哪个班的平均水平较高；

(2)若数学成绩不低于120分，则称为“优秀”，求从这20名学生中随机选取三人，至多有一人是优秀的概率；

(3)以这20人的样本数据来估计整个学校的总体成绩，若从该校（人数很多）任选三人，记表示抽到优秀学生的人数，求的分布列及数学期望.

（1）在空间，求与定点距离等于1的点所围成的几何体的体积和表面积；

（2）在空间，线段(包括端点)的长等于1，求到线段的距离等于1的点所围成的几何体的体积和表面积；

（3）在空间，记边长为1的正方形区域(包括边界及内部的点)为，求到距离等于1的点所围成的几何体的体积和表面积.

【题目】（1）用篱笆围一个面积为的矩形菜园，当这个矩形的边长为多少时，所用篱笆最短？最短篱笆的长度是多少？

（2）用一段长为的篱笆围成一个矩形菜园，当这个矩形的边长为多少时，菜园的面积最大？最大面积是多少？

【题目】焦距为的椭圆()，如果满足“”，则称此椭圆为“等差椭圆”.

（1）如果椭圆()是“等差椭圆”，求的值；

（2）如果椭圆 ()是“等差椭圆”，过作直线与此“等差椭圆”只有一个公共点，求此直线的斜率；

（3）椭圆()是“等差椭圆”，如果焦距为12，求此“等差椭圆”的方程；

（4）对于焦距为12的“等差椭圆”，点为椭圆短轴的上顶点，为椭圆上异于点的任一点，为关于原点的对称点(也异于)，直线分别与轴交于两点，判断以线段为直径的圆是否过定点？说明理由.

【题目】设是一些互不相同的四元数组的集合，其中，或．已知的元素个数不超过15，且满足：若、，则、，其中，，．求集合元素个数的最大值．

【题目】已知双曲线的离心率为2，过点、斜率为1的直线与双曲线交于、两点且，.

（1）求双曲线方程。

（2）设为双曲线右支上动点，为双曲线的右焦点，在轴负半轴上是否存在定点，使得？若存在，求出点的坐标；若不存在，请说明理由。

（1）C、E、0、F四点共圆；

（2）A、0、F三点共线；

（3）EA=EF。

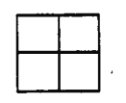
【题目】如图，记从“田字型”网格(由四个边长为1的正方形构成)的九个交点中任取三点构成的三角形面积为ξ(当所取的三点共线时，ξ=0)，则ξ的数学期望=_________。

【题目】已知三棱锥(如图一)的平面展开图(如图二)中，为边长等于的正方形，△和△均为正三角形，在三棱锥中，

（1）求证：；

（2）求与平面所成的角的大小；

（3）求二面角的大小.

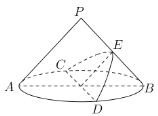
【题目】我们知道：用平行于圆锥母线的平面(不过顶点)截圆锥，则平面与圆锥侧面的交线是抛物线一部分，如图，在底面半径和高均为2的圆锥中，是底面圆的两条互相垂直的直径，是母线的中点，已知过与的平面与圆锥侧面的交线是以为顶点的圆锥曲线的一部分，则该圆锥曲线的焦点到其准线的距离等于__________.