
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 且
且![]() ,
,![]() .
.
(1)若函数f(x)与g(x)有相同的极值点(极值点是指函数取极值时对应的自变量的值),求k的值;
(2)当m>0,k = 0时,求证:函数![]() 有两个不同的零点;
有两个不同的零点;
(3)若![]() ,记函数
,记函数![]() ,若
,若![]() ,使
,使![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某鲜花小镇圈定一块半径为1百米的圆形荒地,准备建成各种不同鲜花景观带.为了便于游客观赏,准备修建三条道路AB,BC,CA,其中A,B,C分别为圆上的三个进出口,且A,B分别在圆心O的正东方向与正北方向上,C在圆心O南偏西某一方向上.在道路AC与BC之间修建一条直线型水渠MN种植水生观赏植物黄鸢尾(其中点M,N分别在BC和CA上,且M在圆心O的正西方向上,N在圆心O的正南方向上),并在区域MNC内种植柳叶马鞭草.
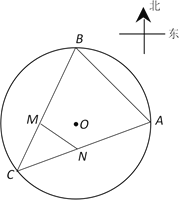
(1)求水渠MN长度的最小值;
(2)求种植柳叶马鞭草区域MNC面积的最大值(水渠宽度忽略不计).
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比![]() .
.
(1)设圆![]() 求过
求过![]() (2,0)的直线关于圆
(2,0)的直线关于圆![]() 的距离比
的距离比![]() 的直线方程;
的直线方程;
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() (0,3)且直线
(0,3)且直线![]() =
= ![]() 关于圆
关于圆![]() 的距离比
的距离比![]() ,求此圆的
,求此圆的![]() 的方程;
的方程;
(3)是否存在点![]() ,使过
,使过![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,动圆
中,动圆![]() 与圆
与圆![]() 外切,且圆
外切,且圆![]() 与直线
与直线![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)设过定点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问:在曲线
两点,试问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值?若存在,求出点
的斜率之和为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
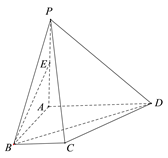
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一种大型商品,![]() 、
、![]() 两地都有出售,且价格相同,现
两地都有出售,且价格相同,现![]() 地的居民从
地的居民从![]() 、
、![]() 两地之一购得商品后回运的运费是:
两地之一购得商品后回运的运费是:![]() 地每公里的运费是
地每公里的运费是![]() 地运费的
地运费的![]() 倍,已知
倍,已知![]() 、
、![]() 两地相距
两地相距![]() ,居民选择
,居民选择![]() 或
或![]() 地购买这种商品的标准是:包括运费和价格的总费用较低.
地购买这种商品的标准是:包括运费和价格的总费用较低.
(1)求![]() 地的居民选择
地的居民选择![]() 地或
地或![]() 地购物总费用相等时,点
地购物总费用相等时,点![]() 所在曲线的形状;
所在曲线的形状;
(2)指出上述曲线内、曲线外的居民应如何选择购货地点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com