【题目】某工厂在生产产品时需要用到长度为的型和长度为的型两种钢管.工厂利用长度为的钢管原材料，裁剪成若干型和型钢管，假设裁剪时损耗忽略不计，裁剪后所剩废料与原材料的百分比称为废料率.

（1）要使裁剪的废料率小于，共有几种方案剪裁？请写出每种方案中分别被裁剪型钢管和型钢管的根数；

（2）假设一根型钢管和一根型钢管能成为一套毛胚，假定只能按（1）中的那些方案裁剪，若工厂需要生产套毛胚，则至少需要采购多少根长度为的钢管原材料？最终的废料率为多少？

【题目】（1）已知是定义在上的奇函数，求实数、的值；

（2）已知是定义在上的函数，求实数的取值范围.

【题目】已知、、、是同一平面上不共线的四点，若存在一组正实数、、，使得，则三个角、、（ ）

A. 都是钝角B. 至少有两个钝角

C. 恰有两个钝角D. 至多有两个钝角

【题目】由无理数论引发的数字危机一直延续到19世纪，直到1872年，德国数学家戴德金从连续性的要求出发，用有理数的“分割”来定义无理数（史称戴德金分割），并把实数理论建立在严格的科学基础上，才结束了无理数被认为“无理”的时代，也结束了持续2000多年的数学史上的第一次大危机，所谓戴德金分割，是指将有理数集划分为两个非空的子集与，且满足，，中的每一个元素都小于中的每一个元素，则称为戴德金分割.试判断，对于任一戴德金分割，下列选项中，可能成立的是____．

①没有最大元素，有一个最小元素；②没有最大元素，也没有最小元素；

③有一个最大元素，有一个最小元素；④有一个最大元素，没有最小元素.

【题目】关于的方程恰有3个实数根，，，则__________．

【题目】设，若数列满足：对所有，，且当时，，则称为“数列”，设R，函数，数列满足，（）.

（1）若，而是数列，求的值；

（2）设，证明：存在，使得是数列，但对任意，都不是数列；

（3）设，证明：对任意，都存在，使得是数列.

【题目】（1）已知实数，，，则的最小值是______．

（2）正项等比数列中，存在两项使得，且，则的最小值为______.

（3）设正实数满足，则的最小值为_______．

【题目】已知抛物线，直线、（），与恰有一个公共点，与恰有一个公共点，与交于点.

（1）当时，求点到准线的距离；

（2）当与不垂直时，求的取值范围；

（3）设是平面上一点，满足且，求和的夹角大小.

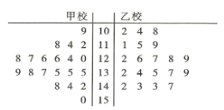
（1）试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数；

（2）若把数学成绩不低于135分的记作数学成绩优秀，根据茎叶图中的数据，判断是否有90的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关；

（3）若从这40名学生中选取数学成绩在的学生，用分层抽样的方式从甲乙两校中抽取5人，再从这5人中随机抽取3人分析其失分原因，求这3人中恰有2人是乙校学生的概率．

参考公式与临界值表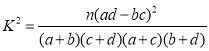：，其中．

(1)若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；

(2)若从亚洲国家和欧洲国家中各选1个，求这两个国家包括A1，但不包括B1的概率．