
科目: 来源: 题型:
【题目】改革开放以来,伴随着我国经济持续增长,户均家庭教育投入![]() 户均家庭教育投入是指一个家庭对家庭成员教育投入的总和
户均家庭教育投入是指一个家庭对家庭成员教育投入的总和![]() 也在不断提高
也在不断提高![]() 我国某地区2012年至2018年户均家庭教育投入
我国某地区2012年至2018年户均家庭教育投入![]() 单位:千元
单位:千元![]() 的数据如表:
的数据如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
户均家庭教育投入y |
|
|
|
|
|
|
|
![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: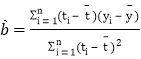 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,
,![]() 交
交![]() 正半轴于
正半轴于![]() 点,
点,![]() 交
交![]() 正半轴于
正半轴于![]() 点,则线段
点,则线段![]() 中点
中点![]() 轨迹方程为_______________________;过原点
轨迹方程为_______________________;过原点![]() 与
与![]() 、
、![]() 、
、![]() 四点的圆半径的最小值为______________.
四点的圆半径的最小值为______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放以来,我国经济持续高速增长![]() 如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值
如图给出了我国2003年至2012年第二产业增加值与第一产业增加值的差值![]() 以下简称为:产业差值
以下简称为:产业差值![]() 的折线图,记产业差值为
的折线图,记产业差值为![]() 单位:万亿元
单位:万亿元![]() .
.
![]() 求出y关于年份代码t的线性回归方程;
求出y关于年份代码t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2003年至2012年我国产业差值的变化情况,并预测我国产业差值在哪一年约为34万亿元;
中的回归方程,分析2003年至2012年我国产业差值的变化情况,并预测我国产业差值在哪一年约为34万亿元;
![]() 结合折线图,试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差
结合折线图,试求出除去2007年产业差值后剩余的9年产业差值的平均值及方差![]() 结果精确到
结果精确到![]() .
.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: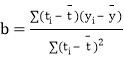 ,
,![]() .
.
样本方差公式:![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目: 来源: 题型:
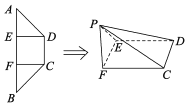
【题目】如图所示,在等腰梯形ABCD中,![]() ,
,![]() ,E,F为AB的三等分点,且
,E,F为AB的三等分点,且![]() 将
将![]() 和
和![]() 分别沿DE、CF折起到A、B两点重合,记为点P.
分别沿DE、CF折起到A、B两点重合,记为点P.
![]() 证明:平面
证明:平面![]() 平面PEF;
平面PEF;
![]() 若
若![]() ,求PD与平面PFC所成角的正弦值.
,求PD与平面PFC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
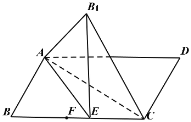
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点且满足
上一点且满足![]() ,
,![]() 是线段
是线段![]() 上一动点,把
上一动点,把![]() 沿
沿![]() 折起得到
折起得到![]() ,使得平面
,使得平面![]() 平面
平面![]() ,分别记
,分别记![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成锐角为
所成锐角为![]() ,则:( )
,则:( )

![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 无实数解”的否命题;
无实数解”的否命题;
(4)命题:“空间中到一个正四面体的六条棱所在的直线距离均相等的点有且只有![]() 个”; 其中真命题( )
个”; 其中真命题( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com