
科目: 来源: 题型:
【题目】已知点![]() 、
、![]() 是双曲线
是双曲线![]() :
:![]() 的左右焦点,其渐近线为
的左右焦点,其渐近线为![]() ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 的法向量为
的法向量为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若双曲线![]() 在第四象限的部分存在一点
在第四象限的部分存在一点![]() 满足
满足![]() ,求
,求![]() 的值及
的值及![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两焦点分别为
的两焦点分别为![]() ,
,![]() ,
,![]() 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足![]() ,过
,过![]() 作倾斜角互补的两直线
作倾斜角互补的两直线![]() 、
、![]() 分别交椭圆于
分别交椭圆于![]() 、
、![]() 两点.
两点.
(1)求![]() 点坐标;
点坐标;
(2)当直线![]() 经过点
经过点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
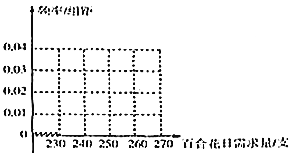
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,请根据(Ⅰ)中频率分布直方图(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率):
(1)写出四月后20天每天百合花需求量![]() 的分布列;
的分布列;
(2)若百合花进货价格与售价均不变,微店从四月十一日起,每天从云南固定空运![]() 支百合花,当
支百合花,当![]() 为多少时,四月后20天每天百合花销售利润
为多少时,四月后20天每天百合花销售利润![]() (单位:元)的期望值最大?
(单位:元)的期望值最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成的),类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,则( )
,则( )
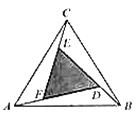
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心为坐标原点,焦点在坐标轴上,且经过点M(4,1),N(2,2).
(1)求椭圆C的方程;
(2)若斜率为1的直线与椭圆C交于不同的两点,且点M到直线l的距离为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一枚质地均匀的硬币连掷三次,事件“恰出现1次反面朝上”的概率记为![]() ,现采用随机模拟的方法估计
,现采用随机模拟的方法估计![]() 的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为
的值:用计算机产生了20组随机数,其中出现“0”表示反面朝上,出现“1”表示正面朝上,结果如下,若出现“恰有1次反面朝上”的频率记为![]() ,则
,则![]() ,
,![]() 分别为( )
分别为( )
111 001 011 010 000 111 111 111 101 010
000 101 011 010 001 011 100 101 001 011
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2xlnx+1.
(1)求曲线y=f(x)在点(e,f(e))处的切线方程;
(2)若关于x的不等式f(x)![]() x2+ax在(
x2+ax在(![]() ,+∞)上恒成立,求实数a的取值范围.
,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com