
科目: 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图:

(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量
附注:
参考数据:![]() ,
,![]() ,
,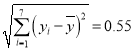 ,
,![]()
参考公式:相关系数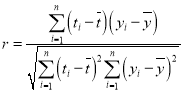 ,回归方程
,回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上点,且
上点,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 相交于另一点
相交于另一点![]() ,且点
,且点![]() 、
、![]() 位于点
位于点![]() 的同侧,当
的同侧,当![]() 面积最大时,求
面积最大时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)将由![]() 代入
代入![]() ,化简即可得到曲线
,化简即可得到曲线![]() 的极坐标方程;(Ⅱ)将
的极坐标方程;(Ⅱ)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]() ,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
试题解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲线![]() 的极坐标方程为
的极坐标方程为![]()
(II)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]()
∴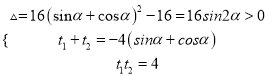 , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
23
【题目】已知![]() 、
、![]() 、
、![]() 均为正实数.
均为正实数.
(Ⅰ)若![]() ,求证:
,求证: ![]()
(Ⅱ)若![]() ,求证:
,求证: ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)将由![]() 代入
代入![]() ,化简即可得到曲线
,化简即可得到曲线![]() 的极坐标方程;(Ⅱ)将
的极坐标方程;(Ⅱ)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]() ,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
试题解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲线![]() 的极坐标方程为
的极坐标方程为![]()
(II)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]()
∴ , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
23
【题目】已知![]() 、
、![]() 、
、![]() 均为正实数.
均为正实数.
(Ⅰ)若![]() ,求证:
,求证: ![]()
(Ⅱ)若![]() ,求证:
,求证: ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应市政府迎接全国文明城市创建活动的号召,某学校组织学生举行了文明城市创建知识类竞赛,为了了解本次竞赛中学生的成绩情况,从中抽取![]() 名学生的分数(满分为100分,得分取正整数,抽取学生的分数均在
名学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本进行统计,按照
之内)作为样本进行统计,按照![]() 分成
分成![]() 组,并作出如下频率分布直方图,已知得分在
组,并作出如下频率分布直方图,已知得分在![]() 的学生有
的学生有![]() 人.
人.

![]() 求频率分布直方图中的的
求频率分布直方图中的的![]() 值,并估计学生分数的众数、平均数和中位数:
值,并估计学生分数的众数、平均数和中位数:
![]() 如果从
如果从![]() 三个分数段的学生中,按分层抽样的方法抽取
三个分数段的学生中,按分层抽样的方法抽取![]() 人参与座谈会,然后再从
人参与座谈会,然后再从![]() 两组选取的人中随机抽取
两组选取的人中随机抽取![]() 人作进一步的测试,求这
人作进一步的测试,求这![]() 人中恰有一人得分在
人中恰有一人得分在![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为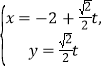 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com