（1）根据以上数据建立一个2×2列联表；

（2）判断性别与休闲方式是否有关系．

下面临界值表供参考：

（参考公式：K2=）

【题目】已知函数

（1）若，，若的单调区间；

（2）当时，若存在唯一的零点，且，其中，求.

（参考数据：，）

【题目】已知椭圆的离心率为，以椭圆的长轴和短轴为对角线的四边形的面积为.

（1）求椭圆的方程；

（2）若直线与椭圆相交于，两点，设为椭圆上一动点，且满足（为坐标原点）.当时，求的最大值.

【题目】端午佳节旌旗胜，龙舟竞渡展雄风.端午龙舟竞渡活动是我国的民间传统习俗，龙舟精神激发着汕尾海陆丰老区人民敢为人先、奋发有为的勇气.每年在粽叶飘香的端午节到来的前一天，汕尾市都将在美丽的品清湖畔举行龙舟锦标赛，他们将在这片碧蓝的品清湖上挥桨劈浪，奋勇争先，一往无前的龙舟精神，该活动也为市民提供了难得的视觉盛宴.某商家为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了6月2日至6月6日的白天平均气温（℃）与该奶茶店的这种饮料销量（杯），得到如下数据：

（1）先从这五组数据中抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；

（2）请根据所给五组数据，求出了关于的线性回归方程；若气象台预报6月7日白天的平均气温为35℃，根据线性回归方程预测该奶茶店这种饮料的销量（取整数）.

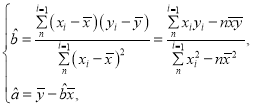附：线性回归方程中，其中，为样本平均值.

A.4B.5C.6D.8

【题目】日本数学家角谷静夫发现的“ 猜想”是指：任取一个自然数，如果它是偶数，我们就把它除以，如果它是奇数我们就把它乘再加上，在这样一个变换下，我们就得到了一个新的自然数。如果反复使用这个变换，我们就会得到一串自然数，猜想就是：反复进行上述运算后，最后结果为，现根据此猜想设计一个程序框图如图所示，执行该程序框图输入的，则输出值为（ ）

A. B. C. D.

【题目】设等差数列的公差为前项和为且则的取值范围是_________.

【题目】已知数列满足，，.

（1）若，试问是否存在实数，使得数列是等比数列？若存在，求出的值；若不存在，请说明理由；

（2）在（1）的条件下，求数列的通项公式.

(1)若∠POB=θ，试将四边形OPDC的面积y表示为关于θ的函数；

(2)求四边形OPDC面积的最大值．

【题目】已知等差数列的前项的和为，公差，若，，成等比数列，；数列满足：对于任意的，等式都成立.

（1）求数列的通项公式；

（2）证明：数列是等比数列；

（3）若数列满足，试问是否存在正整数，（其中），使，，成等比数列.