
科目: 来源: 题型:
【题目】已知数列![]() 为等比数列,
为等比数列,![]() 公比为
公比为![]()
![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() 求
求![]()
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() 使得对任意正整数
使得对任意正整数![]() 不等式
不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: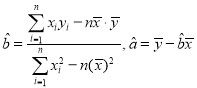
查看答案和解析>>
科目: 来源: 题型:
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
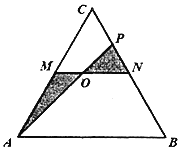
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
科目: 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:

(1)求频率直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中人选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于![]() 的偶数可以表示为两个素数的和”,如
的偶数可以表示为两个素数的和”,如![]() .现从不超过
.现从不超过![]() 的素数中,随机选取两个不同的数(两个数无序).(注:不超过
的素数中,随机选取两个不同的数(两个数无序).(注:不超过![]() 的素数有
的素数有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)列举出满足条件的所有基本事件;
(2)求“选取的两个数之和等于![]() ”事件发生的概率.
”事件发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F为椭圆C:![]() 的左焦点,过F作两条互相垂直的直线
的左焦点,过F作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与C交于A,B两点,直线
与C交于A,B两点,直线![]() 与C交于D,E两点,则四边形ADBE的面积最小值为( )
与C交于D,E两点,则四边形ADBE的面积最小值为( )
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】双十一购物狂欢节,源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了
日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了![]() 份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
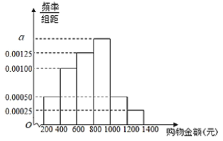
(1)求![]() 的值;
的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围 |
|
|
|
|
|
|
商家优惠(元) |
|
|
|
|
|
|
如果你是购物者,你认为哪种方案优惠力度更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com