
科目: 来源: 题型:
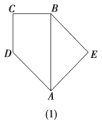
【题目】已知直角梯形![]() 的下底与等腰直角三角形
的下底与等腰直角三角形![]() 的斜边重合,
的斜边重合,![]() 且
且![]() (如图(1)所示),将此图形沿
(如图(1)所示),将此图形沿![]() 折叠成直二面角,连接
折叠成直二面角,连接![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() (如图(2)所示).
(如图(2)所示).
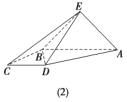
(1)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,说明理由;
;若不存在,说明理由;
(2)在(1)的条件下,求平面![]() 与平面
与平面![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某产品自生产并投入市场以来,生产企业为确保产品质量,决定邀请第三方检测机构对产品进行质量检测,并依据质量指标![]() 来衡量产品的质量.当
来衡量产品的质量.当![]() 时,产品为优等品;当
时,产品为优等品;当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标
时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标![]() 的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
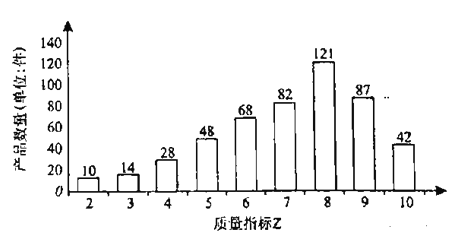
(1)从该企业生产的所有产品中随机抽取1件,求该产品为优等品的概率;
(2)现某人决定购买80件该产品.已知每件成本1000元,购买前,邀请第三方检测机构对要购买的80件产品进行抽样检测.买家、企业及第三方检测机构就检测方案达成以下协议:从80件产品中随机抽出4件产品进行检测,若检测出3件或4件为优等品,则按每件1600元购买,否则按每件1500元购买,每件产品的检测费用250元由企业承担.记企业的收益为![]() 元,求
元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)商场为推广此款产品,现面向意向客户推出“玩游戏,送大奖”活动.客户可根据抛硬币的结果,操控机器人在方格上行进,已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从
,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从![]() 到
到![]() ),若掷出反面,机器人向前移动两格(从
),若掷出反面,机器人向前移动两格(从![]() 到
到![]() ),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第
),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否吸引顾客购买该款产品.
是等比数列,并解释此方案能否吸引顾客购买该款产品.
查看答案和解析>>
科目: 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
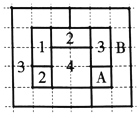
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生,其中8名女生中有3名报考理科,男生中有2名报考文科.
(1)根据以上信息,写出![]() 列联表;
列联表;
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
参考公式:![]()
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设曲线![]() (
(![]() ),
),![]() 是直线
是直线![]() 上的任意一点,过
上的任意一点,过![]() 作
作![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,记
,记![]() 为坐标原点.
为坐标原点.
(1)设![]() ,求
,求![]() 的面积;
的面积;
(2)设![]() 、
、![]() 、
、![]() 的纵坐标依次为
的纵坐标依次为![]() 、
、![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)设点![]() 满足
满足![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上?若存在,求出
上?若存在,求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
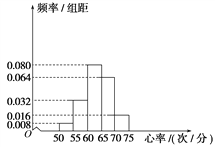
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com