
科目: 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6)先后抛掷两次,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() .
.
(1)设复数![]() (
(![]() 为虚数单位),求事件“
为虚数单位),求事件“![]() 为实数”的概率;
为实数”的概率;
(2)求点![]() 落在不等式组
落在不等式组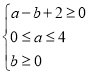 表示的平面区域内(含边界)的概率.
表示的平面区域内(含边界)的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
两位选手,随机调查了20个学生的评分,得到下面的茎叶图:

所得分数 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
(1)通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计![]() 两位选手中哪位选手直接晋级的概率更大,并说明理由.
两位选手中哪位选手直接晋级的概率更大,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: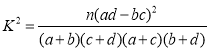 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,动点
轴,动点![]() 在
在![]() 上,且满足
上,且满足![]() (
(![]() 为坐标原点),记点
为坐标原点),记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知定点![]() ,
,![]() ,
,![]() 为曲线
为曲线![]() 上一点,直线
上一点,直线![]() 交曲线
交曲线![]() 于另一点
于另一点![]() ,且点
,且点![]() 在线段
在线段![]() 上,直线
上,直线![]() 交曲线
交曲线![]() 于另一点
于另一点![]() ,求
,求![]() 的内切圆半径
的内切圆半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,直线l过点P(1,1),且倾斜角α=![]() .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com