
科目: 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意
,且对任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,则称数列
,则称数列![]() 为“T”数列.
为“T”数列.
(1)证明:正项无穷等差数列![]() 是“T”数列;
是“T”数列;
(2)记正项等比数列![]() 的前n项之和为
的前n项之和为![]() ,若数列
,若数列![]() 是“T”数列,求数列
是“T”数列,求数列![]() 公比的取值范围;
公比的取值范围;
(3)若数列![]() 是“T”数列,且数列
是“T”数列,且数列![]() 的前n项之和
的前n项之和![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,(
,(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求实数am的值;
,求实数am的值;
(2)关于x的方程![]() 能否有三个不同的实根?证明你的结论;
能否有三个不同的实根?证明你的结论;
(3)若![]() 对任意
对任意![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
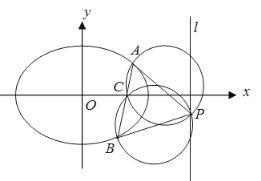
【题目】如图所示,已知椭圆:![]() (
(![]() )的离心率为
)的离心率为![]() ,右准线方程是直线l:
,右准线方程是直线l:![]() ,点P为直线l上的一个动点,过点P作椭圆的两条切线
,点P为直线l上的一个动点,过点P作椭圆的两条切线![]()
![]() ,切点分别为AB(点A在x轴上方,点B在x轴下方).
,切点分别为AB(点A在x轴上方,点B在x轴下方).
(1)求椭圆的标准方程;
(2)①求证:分别以![]()
![]() 为直径的两圆都恒过定点C;
为直径的两圆都恒过定点C;
②若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
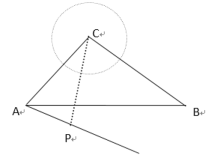
【题目】某工厂C发生爆炸出现毒气泄漏,已知毒气以圆形向外扩散,且半径以每分钟![]() 的速度增大. 一所学校A,位于工厂C南偏西
的速度增大. 一所学校A,位于工厂C南偏西![]() ,且与工厂相距
,且与工厂相距![]() .消防站B位于学校A的正东方向,且位于工厂C南偏东
.消防站B位于学校A的正东方向,且位于工厂C南偏东![]() ,立即以每分钟
,立即以每分钟![]() 的速度沿直线
的速度沿直线![]() 赶往工厂C救援,同时学校组织学生P从A处沿着南偏东
赶往工厂C救援,同时学校组织学生P从A处沿着南偏东![]() 的道路,以每分钟
的道路,以每分钟![]() 的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com