
科目: 来源: 题型:
【题目】函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)若![]() ,
,![]() 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ax2–a–lnx,g(x)=![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)证明:当x>1时,g(x)>0;
(Ⅲ)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 到抛物线C:y2=2px
到抛物线C:y2=2px![]() 准线的距离为2.
准线的距离为2.
(Ⅰ)求C的方程及焦点F的坐标;
(Ⅱ)设点P关于原点O的对称点为点Q,过点Q作不经过点O的直线与C交于两点A,B,直线PA,PB,分别交x轴于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
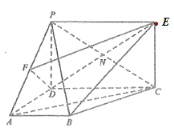
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知i为虚数单位,下列说法中正确的是( )
A.若复数z满足![]() ,则复数z对应的点在以
,则复数z对应的点在以![]() 为圆心,
为圆心,![]() 为半径的圆上
为半径的圆上
B.若复数z满足![]() ,则复数
,则复数![]()
C.复数的模实质上就是复平面内复数对应的点到原点的距离,也就是复数对应的向量的模
D.复数![]() 对应的向量为
对应的向量为![]() ,复数
,复数![]() 对应的向量为
对应的向量为![]() ,若
,若![]() ,则
,则![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(多选)已知函数![]() ,其中正确结论的是( )
,其中正确结论的是( )
A.当![]() 时,函数
时,函数![]() 有最大值.
有最大值.
B.对于任意的![]() ,函数
,函数![]() 一定存在最小值.
一定存在最小值.
C.对于任意的![]() ,函数
,函数![]() 是
是![]() 上的增函数.
上的增函数.
D.对于任意的![]() ,都有函数
,都有函数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com