
【题目】函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点.(极值点是指函数取极值时对应的自变量的值)
的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)若![]() ,
,![]() 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)b=![]() (a>3);(2)(3,6]
(a>3);(2)(3,6]
【解析】
(1)求导得到g(x)=f′(x)=3x2+2ax+b,计算函数单调性,故f(﹣![]() )=0,计算得到b=
)=0,计算得到b=![]() ,再计算a>3得到答案.
,再计算a>3得到答案.
(2)f′(x)的极小值为f′(﹣![]() )=b﹣
)=b﹣![]() ,设x1,x2是y=f(x)的两个极值点,则x1+x2=
,设x1,x2是y=f(x)的两个极值点,则x1+x2=![]() ,x1x2=
,x1x2=![]() ,f(x1)+f(x2)=
,f(x1)+f(x2)=![]() ﹣
﹣![]() +2,得到所以b﹣
+2,得到所以b﹣![]() +
+![]() ﹣
﹣![]() +2≥﹣
+2≥﹣![]() ,解得答案.
,解得答案.
(1)因为f(x)=x3+ax2+bx+1,所以g(x)=f′(x)=3x2+2ax+b,
g′(x)=6x+2a,令g′(x)=0,解得x=﹣![]() .
.
由于当x>﹣![]() 时g′(x)>0,g(x)=f′(x)单调递增;
时g′(x)>0,g(x)=f′(x)单调递增;
当x<﹣![]() 时g′(x)<0,g(x)=f′(x)单调递减;
时g′(x)<0,g(x)=f′(x)单调递减;
所以f′(x)的极小值点为x=﹣![]() ,由于导函数f′(x)的极值点是原函数f(x)的零点,
,由于导函数f′(x)的极值点是原函数f(x)的零点,
所以f(﹣![]() )=0,即﹣
)=0,即﹣![]() ﹣
﹣![]() +1=0,所以b=
+1=0,所以b=![]() (a>0).
(a>0).
因为f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,所以f′(x)=3x2+2ax+b=0有实根,
所以4a2﹣12b>0,即a2﹣![]() ﹣
﹣![]() >0,解得a>3,所以b=
>0,解得a>3,所以b=![]() (a>3).
(a>3).
(2)f′(x)的极小值为f′(﹣![]() )=b﹣
)=b﹣![]() ,
,
设x1,x2是y=f(x)的两个极值点,则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
所以f(x1)+f(x2)=![]() +
+![]() +a(
+a(![]() +
+![]() )+b(x1+x2)+2
)+b(x1+x2)+2
=(x1+x2)[(x1+x2)2﹣3x1x2]+a[(x1+x2)2﹣2x1x2]+b(x1+x2)+2=![]() ﹣
﹣![]() +2,
+2,
又因为f(x),f′(x)这两个函数的所有极值之和不小于﹣![]() ,
,
所以b﹣![]() +
+![]() ﹣
﹣![]() +2=
+2=![]() ﹣
﹣![]() ≥﹣
≥﹣![]() ,因为a>3,所以2a3﹣63a﹣54≤0,
,因为a>3,所以2a3﹣63a﹣54≤0,
所以2a(a2﹣36)+9(a﹣6)≤0,所以(a﹣6)(2a2+12a+9)≤0,
由于a>3时2a2+12a+9>0,所以a﹣6≤0,解得a≤6,所以a的取值范围是(3,6].


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】居民消费价格指数(Consumer Price Index,简称![]() ),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月
),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月![]() 数据同比和环比涨跌幅折线图:
数据同比和环比涨跌幅折线图:
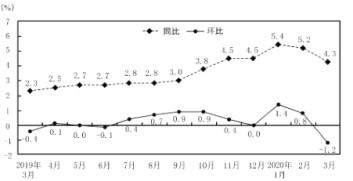
(注:同比![]() ,同比涨跌幅
,同比涨跌幅![]() ,环比
,环比![]() ,环比涨跌幅
,环比涨跌幅![]() ),则下列说法正确的是( )
),则下列说法正确的是( )
A.2019年12月与2018年12月![]() 相等
相等
B.2020年3月比2019年3月![]() 上涨4.3%
上涨4.3%
C.2019年7月至2019年11月![]() 持续增长
持续增长
D.2020年1月至2020年3月![]() 持续下降
持续下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.
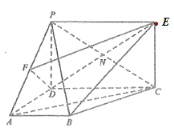
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击中目标得
次,射击中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率;
局的得分恰好相等的概率;
(2)从甲,乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com