
科目: 来源: 题型:
【题目】(1)直线![]() 在矩阵
在矩阵![]() 所对应的变换
所对应的变换![]() 下得到直线
下得到直线![]() ,求
,求![]() 的方程.
的方程.
(2)已知点![]() 是曲线
是曲线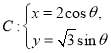 (
(![]() 为参数,
为参数,![]() )上一点,
)上一点,![]() 为坐标原点直线
为坐标原点直线![]() 的倾斜角为
的倾斜角为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】在无穷数列![]() 中,
中,![]() ,记
,记![]() 前
前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,令
,令![]() .
.
(1)若![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
①求![]() ;
;
②是否存在正整数![]() 满足
满足![]() ?若存在,请求出这样的
?若存在,请求出这样的![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
(2)若数列![]() 是等比数列,求证:数列
是等比数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上具有单调性,求
上具有单调性,求![]() 的取值范围;
的取值范围;
(3)若函数![]()
![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,且
,且![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 与椭圆的左、右顶点连线的斜率之积为
与椭圆的左、右顶点连线的斜率之积为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 上存在两点
上存在两点![]() ,使得
,使得![]() 的垂心(三角形三条高的交点)恰为坐标原点
的垂心(三角形三条高的交点)恰为坐标原点![]() ,试求直线
,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人承包了一块矩形土地![]() 用来种植草莓,其中
用来种植草莓,其中![]() m,
m,![]() m.现规划建造如图所示的半圆柱型塑料薄膜大棚
m.现规划建造如图所示的半圆柱型塑料薄膜大棚![]() 个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米
个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米![]() 元;另外,还需在每个大棚之间留下
元;另外,还需在每个大棚之间留下![]() m宽的空地用于建造排水沟与行走小路(如图中
m宽的空地用于建造排水沟与行走小路(如图中![]() m),这部分建设造价为每平方米
m),这部分建设造价为每平方米![]() 元.
元.
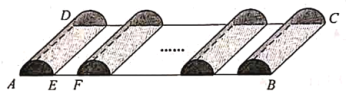
(1)当![]() 时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留
时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留![]() )
)
(2)试确定大棚的个数,使得上述两项费用的和最低?(本小题计算中![]() 取
取![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com