
科目: 来源: 题型:
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
查看答案和解析>>
科目: 来源: 题型:
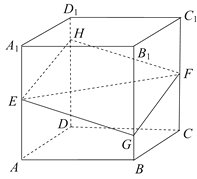
【题目】如图,正方体![]() 的棱长为
的棱长为![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() .给出以下四个命题:
.给出以下四个命题:
①平面![]() 与平面
与平面![]() 所成角的最大值为45°;
所成角的最大值为45°;
②四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
③四棱锥![]() 的体积为
的体积为![]() ;
;
④点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() .
.
其中命题正确的序号为( )
A.②③④B.②③C.①②④D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】皮埃尔·德·费马,法国律师和业余数学家,被誉为“业余数学家之王”,对数学界做出了重大贡献,其中在1636年发现了:若![]() 是质数,且
是质数,且![]() 互质,那么
互质,那么![]() 的
的![]() 次方除以
次方除以![]() 的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集
的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集![]() 中任取两个数,其中一个作为
中任取两个数,其中一个作为![]() ,另一个作为
,另一个作为![]() ,则所取两个数不符合费马小定理的概率为( )
,则所取两个数不符合费马小定理的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元,未售出的产品,每盒亏损
元,未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.

(1)根据直方图估计这个开学季内市场需求量![]() 的众数和平均数;
的众数和平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为增进市民的环保意识,某市有关部门面向全体市民进行了一次环保知识的微信问卷测试活动,每位市民仅有一次参与问卷测试机会.通过抽样,得到参与问卷测试的1000人的得分数据,制成频率分布直方图如图所示.

(1)估计成绩得分落在[86,100]中的概率.
(2)设这1000人得分的样本平均值为![]() .
.
(i)求![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(ii)有关部门为参与此次活动的市民赠送20元或10元的随机话费,每次获赠20元或10元的随机话费的概率分别为![]() 和
和![]() .得分不低于
.得分不低于![]() 的可获赠2次随机话费,得分低于
的可获赠2次随机话费,得分低于![]() 的可获赠1次随机话费.求一位市民参与这次活动获赠话费
的可获赠1次随机话费.求一位市民参与这次活动获赠话费![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() ,
,![]() 实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
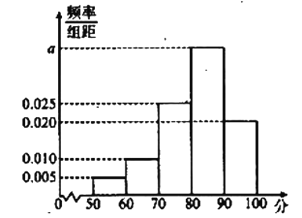
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)用样本估计总体,以频率作为概率,若在![]() ,
,![]() 两块试验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
两块试验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(Ⅲ)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | <>0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: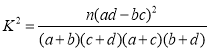 ,其中
,其中![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com