
科目: 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作斜率为
作斜率为![]() 的直线恰好与椭圆
的直线恰好与椭圆![]() 有且仅有一个公共点.
有且仅有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于不同的两点
于不同的两点![]() ,
,![]() ,是否存在常数
,是否存在常数![]() ,使
,使![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
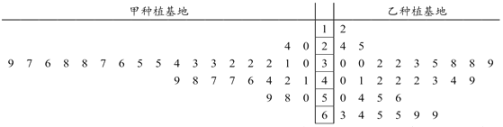
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】为建设美丽新农村,某村对本村布局重新进行了规划,其平面规划图如图所示,其中平行四边形![]() 区域为生活区,
区域为生活区,![]() 为横穿村庄的一条道路,
为横穿村庄的一条道路,![]() 区域为休闲公园,
区域为休闲公园,![]() ,
,![]() ,
,![]() 的外接圆直径为
的外接圆直径为![]() .
.

(1)求道路![]() 的长;
的长;
(2)该村准备沿休闲公园的边界修建栅栏,以防村中的家畜破坏公园中的绿化,试求栅栏总长的最大值.
查看答案和解析>>
科目: 来源: 题型:
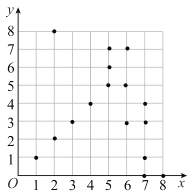
【题目】甲、乙、丙、丁四人进行一项益智游戏,方法如下:第一步:先由四人看着平面直角坐标系中方格内的16个棋子(如图所示),甲从中记下某个棋子的坐标;第二步:甲分别告诉其他三人:告诉乙棋子的横坐标.告诉丙棋子的纵坐标,告诉丁棋子的横坐标与纵坐标相等;第三步:由乙、丙、丁依次回答.对话如下:“乙先说我无法确定.丙接着说我也无法确定.最后丁说我知道”.则甲记下的棋子的坐标为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】“互倒函数”的定义如下:对于定义域内每一个![]() ,都有
,都有![]() 成立,若现在已知函数
成立,若现在已知函数![]() 是定义域在
是定义域在![]() 的“互倒函数”,且当
的“互倒函数”,且当![]() 时,
时,![]() 成立.若函数
成立.若函数![]() (
(![]() )都恰有两个不同的零点,则实数
)都恰有两个不同的零点,则实数![]() 的取值范围是( )
的取值范围是( )
A.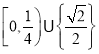 B.
B.![]() C.
C.![]() D.
D.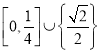
查看答案和解析>>
科目: 来源: 题型:
【题目】毕达哥拉斯树是由毕达哥拉斯根据“勾股定理”所画出来的一个可以无限重复的图形,也叫“勾股树”,其是由一个等腰直角三角形分别以它的每一条边向外作正方形而得到.图1所示是第1代“勾股树”,重复图1的作法,得到第2代“勾股树”(如图2),如此继续.若“勾股树”上共得到8191个正方形,设初始正方形的边长为1,则最小正方形的边长为( )
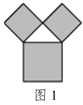
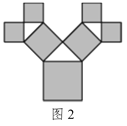
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() ,在以O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为
,在以O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)设曲线C与直线l的交点为A、B,求弦AB的中点P的直角坐标;
(2)动点Q在曲线C上,在(1)的条件下,试求△OPQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com