【题目】如图，在三棱锥中，已知平面，是边长为的正三角形，、分别为、的中点.

（1）若，求直线与所成角的余弦值；

（2）若平面平面，求的长.

【题目】已知函数，，.

（1）求函数的单调增区间；

（2）令，且函数有三个彼此不相等的零点0，m，n，其中.

①若，求函数在处的切线方程；

②若对，恒成立，求实数t的去取值范围.

【题目】如图，某湿地公园的鸟瞰图是一个直角梯形，其中：，，，长1千米，长千米，公园内有一个形状是扇形的天然湖泊，扇形以长为半径，弧为湖岸，其余部分为滩地，B，D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道：线段线段弧，其中Q在线段上（异于线段端点），与弧相切于P点（异于弧端点］根据市场行情，段的建造费用是每千米10万元，湖岸段弧的建造费用是每千米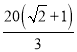万元（步行道的宽度不计），设为弧度观光步行道的建造费用为万元.

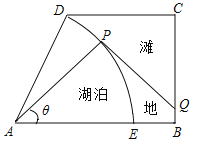
（1）求步行道的建造费用关于的函数关系式，并求其走义域；

（2）当为何值时，步行道的建造费用最低？

【题目】已知函数，.

（1）讨论在区间上的单调性；

（2）若时，，求整数的最小值.

【题目】如图，正四棱锥的底面边长为，、分别为、的中点.

（1）当时，证明：平面平面；

（2）若平面与底面所成锐二面角为，求直线与平面所成角的正弦值.

【题目】设.

（1）若，且为函数的一个极值点，求函数的单调递增区间；

（2）若，且函数的图象恒在轴下方，其中是自然对数的底数，求实数的取值范围.

【题目】已知椭圆的左、右焦点分别为，离心率为，为椭圆上一动点（异于左右顶点），面积的最大值为．

（1）求椭圆的方程；

（2）若直线与椭圆相交于点两点，问轴上是否存在点，使得是以为直角顶点的等腰直角三角形？若存在，求点的坐标；若不存在，请说明理由．

（Ⅰ）若以“年龄45岁为分界点”，由以上计数据完成下面列联表，并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关；

（Ⅱ）若从年龄在的被调查人中按照赞成与不赞成分层抽样，抽取5人进行追踪调查，在5人中抽取3人做专访，求3人中不赞成使用微信支付的人数的分布列和期望值.

参考数据：

，其中.

【题目】正三棱锥，为中点，，，过的平面截三棱锥的外接球所得截面的面积范围为________．

【题目】已知函数，（其中）的图象关于点成中心对称，且与点相邻的一个最低点为，则对于下列判断：

①直线是函数图象的一条对称轴；

②点是函数的一个对称中心；

③函数与的图象的所有交点的横坐标之和为．

其中所有正确的判断是（ ）

A.①②B.①③C.②③D.②