
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: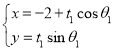 (
(![]() 为参数),曲线
为参数),曲线![]() :
: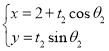 (
(![]() 为参数),且
为参数),且![]() ,点P为曲线
,点P为曲线![]() 与
与![]() 的公共点.
的公共点.
(1)求动点P的轨迹方程;
(2)在以原点O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为![]() ,求动点P到直线l的距离的取值范围.
,求动点P到直线l的距离的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:![]() ,过点
,过点![]() 且互相垂直的两条动直线
且互相垂直的两条动直线![]() ,
,![]() 与抛物线C分别交于P,Q和M,N.
与抛物线C分别交于P,Q和M,N.
(1)求四边形![]() 面积的取值范围;
面积的取值范围;
(2)记线段![]() 和
和![]() 的中点分别为E,F,求证:直线
的中点分别为E,F,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,三角形
,三角形![]() 是等边三角形,平面
是等边三角形,平面![]() 平面
平面![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.
的中点.
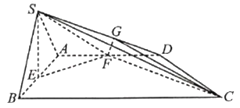
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目: 来源: 题型:
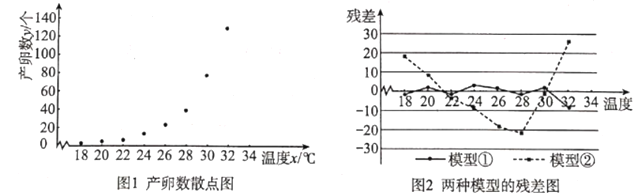
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为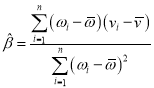 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了解高三年级学生在线学习情况,统计了2020年2月18日-27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.
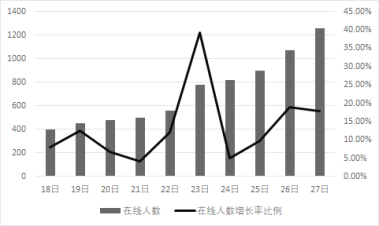
根据组合图判断,下列结论正确的是( )
A.前5天在线学习人数的方差大于后5天在线学习人数的方差
B.前5天在线学习人数的增长比例的极差大于后5天的在线学习人数的增长比例的极差
C.这10天学生在线学习人数的增长比例在逐日增大
D.这10天学生在线学习人数在逐日增加
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(1)求点Q的轨迹(曲线C)的直角坐标方程;
(2)若直线l交曲线C于A,B两点,点![]() 恰好为线段AB的三等分点,求直线l的普通方程.
恰好为线段AB的三等分点,求直线l的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定点![]() ,
,![]() ,动点P为平面上一个动点,且直线SP,TP的斜率之积为
,动点P为平面上一个动点,且直线SP,TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在斜率为![]() 直线l,使得l交轨迹E于M,N两点,且
直线l,使得l交轨迹E于M,N两点,且![]() 恰是
恰是![]() 的重心?若存在,求l的方程;若不存在,说明理由.
的重心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
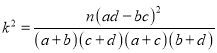
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com