【题目】年初新冠病毒疫情爆发，全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略：先采取甲、乙两套方案教学，并对分别采取两套方案教学的班级的次线上测试成绩进行统计如图所示：

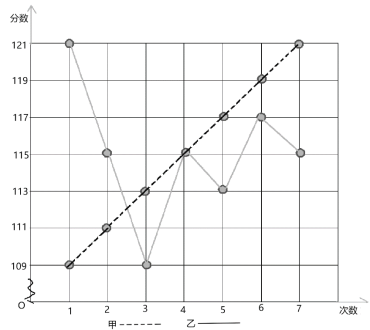
（1）请填写下表（要求写出计算过程）

（2）从下列三个不同的角度对这次方案选择的结果进行

①从平均数和方差相结合看（分析哪种方案的成绩更好）；

②从折线图上两种方案的走势看（分析哪种方案更有潜力）.

【题目】如图所示，已知多面体的底面是边长为2的菱形，底面，且.

（1）证明：平面；

（2）若，求异面直线与所成角的余弦值.

【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看，蜂巢口是由许多正六边形的中空柱状体连接而成，中空柱状体的底部是由三个全等的菱形面构成.如图，在正六棱柱的三个顶点处分别用平面，平面，平面截掉三个相等的三棱锥，，，平面，平面，平面交于点，就形成了蜂巢的结构，如下图（4）所示，

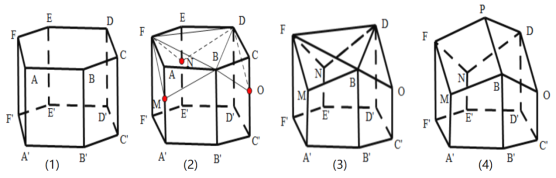
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的，英国数学家麦克劳林通过计算得到菱形的一个内角为，即.以下三个结论①；② ；③四点共面，正确命题的个数为______个；若，，，则此蜂巢的表面积为_______.

【题目】如图，有一种赛车跑道类似“梨形”曲线，由圆弧和线段AB，CD四部分组成，在极坐标系Ox中，A（2，），B（1，），C（1，），D（2，），弧所在圆的圆心分别是（0，0），（2，0），曲线M1是弧，曲线M2是弧．

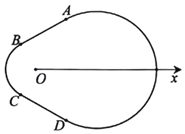
（1）分别写出M1，M2的极坐标方程：

（2）点E，F位于曲线M2上，且，求△EOF面积的取值范围．

（1）当a＝1时，求f（x）的导函数在上的零点个数；

（2）若关于x的不等式2cos（2sinx）+a2x2≤af（x）在（﹣∞，+∞）上恒成立，求实数a的取值范围．

（1）规定预赛成绩不低于80分为优良，若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人，求恰有1人预赛成绩优良的概率；

（2）由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N（μ，σ2），其中μ可近似为样本中的100名学生预赛成绩的平均值（同一组数据用该组区间的中点值代替），且σ2＝362．利用该正态分布，估计全市参加预赛的全体学生中预赛成绩不低于91分的人数；

（3）预赛成绩不低于91分的学生将参加复赛，复赛规则如下：①每人的复赛初始分均为100分；②参赛学生可在开始答题前自行决定答题数量n，每一题都需要“花”掉（即减去）一定分数来获取答题资格，规定答第k题时“花”掉的分数为0.1k（k∈(1，2n））；③每答对一题加1.5分，答错既不加分也不减分；④答完n题后参赛学生的最终分数即为复赛成绩．已知学生甲答对每道题的概率均为0.7，且每题答对与否都相互独立．若学生甲期望获得最佳的复赛成绩，则他的答题数量n应为多少？

（参考数据：；若Z～N（μ，σ2），则P（μ﹣σ＜Z＜μ+σ）≈0.6827，P（μ﹣2σ＜Z＜μ+2σ）≈0.9545，P（μ﹣3σ＜Z＜μ+3σ）≈0.9973．

【题目】已知椭圆C：的短轴长为2，离心率为，左顶点为A，过点A的直线l与C交于另一个点M，且与直线x＝t交于点N．

（1）求椭圆C的方程；

（2）是否存在实数t，使得为定值？若存在，求实数t的值；若不存在，请说明理由．

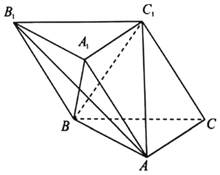
（1）求证：A1B⊥平面AB1C1；

（2）求二面角A1﹣AC1﹣B1的余弦值．

【题目】函数f（x）＝（sinx+cosx）2cos（2x+π）．

（1）求函数f（x）的最小正周期；

（2）已知△ABC的内角A，B，C的对边分别为a，b，c，若，且a＝2，求△ABC的面积．

【题目】已知点F1、F2分别为双曲线C：（a＞0，b＞0）的左、右焦点，点M（x0，y0）（x0＜0）为C的渐近线与圆x2+y2＝a2的一个交点，O为坐标原点，若直线F1M与C的右支交于点N，且|MN|＝|NF2|+|OF2|，则双曲线C的离心率为_____．