【题目】在平面直角坐标系中，动直线交抛物线于A，B两点.

（1）若，证明直线过定点，并求出该定点；

（2）点M为的中点，过点M作与y轴垂直的直线交抛物线于C点；点N为的中点，过点N作与y轴垂直的直线交抛物线于点P.设△的面积，△的面积为.

（i）若过定点，求使取最小值时，直线的方程；

（ii）求的值.

【题目】已知函数.

（1）讨论的单调性；

（2）若，求a的取值范围.

（1）药业公司为了解一新药品对该疾病的疗效，选择了200名患者，随机平均分为两组作为实验组和对照组，实验结束时，有显著疗效的共110人，实验组中有显著疗效的比率为70％.请完成如下的2×2列联表，并根据列联表判断是否有99.9％把握认为该药品对该疾病有显著疗效；

（2）药业公司最多能引进3条新药品的生产线，据测算，公司按如下条件运行生产线：

每运行一条生产线，可产生年利润6000万元，没运行的生产线毎条每年要亏损1000万元.根据该药业公司这10年的统计数据，将患者人数在以上三段的频率视为相应段的概率、假设各年的患者人数相互独立.欲使该药业公司年总利润的期望值达到最大，应引进多少条生产线？

附：参考公式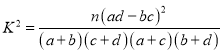：，其中.

【题目】如图，在中，，，，E，F分别为，的中点,是由绕直线旋转得到，连结，，.

（1）证明：平面；

（2）若与平面所成的角为60°，求二面角的余弦值.

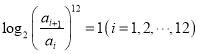【题目】著名物理学家李政道说：“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的，它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例，把八度分成13个半音，使相邻两个半音之间的频率比是常数，如下表所示，其中表示这些半音的频率，它们满足.若某一半音与的频率之比为，则该半音为（ ）

A.B.GC.D.A

【题目】已知函数．

（1），求函数的单调区间：

（2）对于任意，不等式恒成立，求实数的取值范围．

【题目】己知椭圆过点，，是两个焦点．以椭圆的上顶点为圆心作半径为的圆，

（1）求椭圆的方程；

（2）存在过原点的直线，与圆分别交于，两点，与椭圆分别交于，两点（点在线段上），使得，求圆半径的取值范围．

【题目】如图,四棱锥中，，，，，．

（1）求证：平面平面；

（2）在线段上是否存在点，使得平面与平面所成锐二面角为？若存在，求的值；若不存在，说明理由．

【题目】2018年12月18日上午10时，在人民大会堂举行了庆祝改革开放40周年大会．40年众志成城，40年砥砺奋进，40年春风化雨，中国人民用双手书写了国家和民族发展的壮丽史诗．会后，央视媒体平台，收到了来自全国各地的纪念改革开放40年变化的老照片，并从众多照片中抽取了100张照片参加“改革开放40年图片展”，其作者年龄集中在之间，根据统计结果，做出频率分布直方图如下：

（Ⅰ）求这100位作者年龄的样本平均数和样本方差（同一组数据用该区间的中点值作代表）；

（Ⅱ）由频率分布直方图可以认为，作者年龄X服从正态分布，其中近似为样本平

均数，近似为样本方差．

（i）利用该正态分布，求；

（ii）央视媒体平台从年龄在和的作者中，按照分层抽样的方法，抽出了7人参加“纪念改革开放40年图片展”表彰大会，现要从中选出3人作为代表发言，设这3位发言者的年龄落在区间的人数是Y，求变量Y的分布列和数学期望．附：，若，则，

【题目】在锐角△ABC中，a＝2，_______，求△ABC的周长l的范围．

在①(﹣cos，sin)，(cos，sin)，且，②cosA(2b﹣c)＝acosC，③f(x)＝cosxcos(x)，f(A)

注：这三个条件中任选一个，补充在上面问题中并对其进行求解．