
科目: 来源: 题型:
【题目】房屋的天花板上点![]() 处有一光源,
处有一光源,![]() 在地面上的射影为
在地面上的射影为![]() ,在地面上放置正棱锥
,在地面上放置正棱锥![]() ,底面
,底面![]() 接触地面.已知正四棱锥
接触地面.已知正四棱锥![]() 的高为
的高为![]() ,底面
,底面![]() 的边长为
的边长为![]() ,
,![]() 与正方形
与正方形![]() 的中心
的中心![]() 的距离为
的距离为![]() ,又
,又![]() 长为
长为![]() ,则棱锥影子(不包括底面
,则棱锥影子(不包括底面![]() )的面积的最大值为________.
)的面积的最大值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数a与正整数n,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
查看答案和解析>>
科目: 来源: 题型:
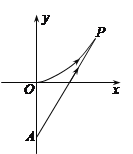
【题目】海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海
里A处,如图. 现假设:①失事船的移动路径可视为抛物线![]() ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发![]() 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为![]() .
.
(1)当![]() 时,写出失事船所在位置P的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
时,写出失事船所在位置P的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目: 来源: 题型:
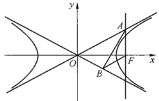
【题目】如图,已知双曲线![]() 的右焦点为F,点A,B分别在C的两条渐近线上,
的右焦点为F,点A,B分别在C的两条渐近线上,![]() 轴,
轴,![]() ,
,![]() (O为坐标原点).
(O为坐标原点).
(1)求双曲线C的方程;
(2)过C上一点![]() 的直线
的直线![]() 与直线AF相交于点M,与直线
与直线AF相交于点M,与直线![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时,![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com