
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,过
,过![]() 的直线与
的直线与![]() 相交于
相交于![]() 两点.
两点.
(1)以![]() 为直径的圆与
为直径的圆与![]() 轴交
轴交![]() 两点,若
两点,若![]() ,求
,求![]() ;
;
(2)点![]() 在
在![]() 上,过点
上,过点![]() 且垂直于
且垂直于![]() 轴的直线与
轴的直线与![]() 分别相交于
分别相交于![]() 两点,证明:
两点,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】法国的数学家费马(PierredeFermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数![]() 时,找不到满足
时,找不到满足![]() 的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取
的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取![]() ,则等式
,则等式![]() 成立的概率为( )
成立的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
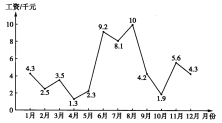
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
科目: 来源: 题型:
【题目】以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:![]() ,曲线C2的参数方程为:
,曲线C2的参数方程为: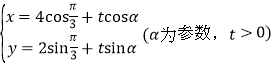 ,点N的极坐标为
,点N的极坐标为![]() .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() 上顶点为A,右焦点为F,直线
上顶点为A,右焦点为F,直线![]() 与圆
与圆![]() 相切,其中
相切,其中![]() .
.
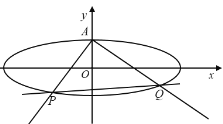
(1)求椭圆的方程;
(2)不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,证明:动直线l过定点,并且求出该定点坐标.
,证明:动直线l过定点,并且求出该定点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
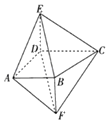
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com