
科目: 来源: 题型:
【题目】为调查某地区被隔离者是否需要社区非医护人员提供帮助,用简单随机抽样方法从该地区调查了500位被隔离者,结果如下:
性别 是否需要 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区被隔离者中,需要社区非医护人员提供帮助的被隔离者的比例;
(2)能否有99%的把握认为该地区的被隔离者是否需要社区非医护人员提供帮助与性别有关?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形![]() 为矩形,
为矩形,![]() ,E为
,E为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,连接
折起,连接![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() ,M为
,M为![]() 的中点,
的中点,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,在翻折过程中,下列四个命题正确的序号是________.
,在翻折过程中,下列四个命题正确的序号是________.
①![]() 平面
平面![]() ;
;
②三棱锥![]() 的体积最大值为
的体积最大值为![]() ;
;
③点M的轨迹是圆的一部分,且![]() ;
;
④一定存在某个位置,使![]() ;
;
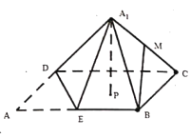
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() :
:![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过![]() 的直线交曲线
的直线交曲线![]() 于不同的
于不同的![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
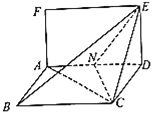
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁-39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”.已知在“经常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
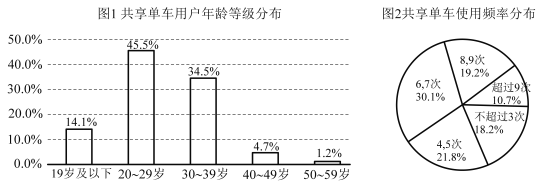
(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列![]() 列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | 120 | ||
不常使用单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
使用共享单车情况与年龄列联表
(2)将(1)中频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
参考数据:独立性检验界值表
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,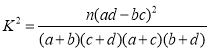 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数1-9的一种方法.例如:3可表示为“≡”,26可表示为“=⊥”,现有6根算筹,据此表示方法,若算筹不能剩余,则可以用1-9这9个数字表示两位数中,能被3整除的概率是( )
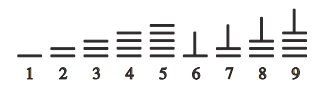
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于无穷数列![]() 的某一项
的某一项![]() ,若存在
,若存在![]() ,有
,有![]() 成立,则称
成立,则称![]() 具有性质
具有性质![]() .
.
(1)设![]() ,若对任意的
,若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,求
,求![]() 的最小值;
的最小值;
(2)设等差数列![]() 的首项
的首项![]() ,公差为
,公差为![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 数列
数列![]() 中的项
中的项![]() 都具有性质
都具有性质![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 的首项
的首项![]() ,当
,当![]() 时,存在
时,存在![]() 满足
满足![]() ,且此数列中恰有一项
,且此数列中恰有一项![]() 不具有性质
不具有性质![]() ,求此数列的前
,求此数列的前![]() 项和的最大值和最小值以及取得最值时对应的
项和的最大值和最小值以及取得最值时对应的![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为M,过点M且斜率为
,上顶点为M,过点M且斜率为![]() 的直线与
的直线与![]() 交于另一点N,过原点的直线l与
交于另一点N,过原点的直线l与![]() 交于P,Q两点
交于P,Q两点
(1)求![]() 周长的最小值:
周长的最小值:
(2)是否存在这样的直线,使得与直线![]() 平行的弦的中点都在该直线上?若存在,求出该直线的方程:若不存在,请说明理由.
平行的弦的中点都在该直线上?若存在,求出该直线的方程:若不存在,请说明理由.
(3)直线l与线段![]() 相交,且四边形
相交,且四边形![]() 的面积
的面积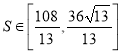 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com