
科目: 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、![]() 后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )

A. 互联网行业从业人员中![]() 后占一半以上
后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 前多
前多
D. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 后多
后多
查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在长方体![]() 中,
中,![]() ,点E是棱
,点E是棱![]() 上的一个动点,若平面
上的一个动点,若平面![]() 交棱
交棱![]() 于点
于点![]() ,给出下列命题:
,给出下列命题:
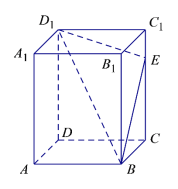
①四棱锥![]() 的体积恒为定值;
的体积恒为定值;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③对于棱![]() 上任意一点
上任意一点![]() ,在棱
,在棱![]() 上均有相应的点
上均有相应的点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得截面四边形
,使得截面四边形![]() 的周长取得最小值.
的周长取得最小值.
其中真命题的是____________.(填写所有正确答案的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点 .
的中点 .
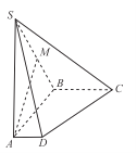
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形![]() 为矩形,
为矩形, ![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,设
,设![]() 的中点为
的中点为![]() ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:
①![]() 平面
平面![]() ,且
,且![]() 的长度为定值
的长度为定值![]() ;
;
②三棱锥![]() 的最大体积为
的最大体积为![]() ;
;
③在翻折过程中,存在某个位置,使得![]() .
.
其中正确命题的序号为__________.(写出所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如果存在常数![]() ,使得数列
,使得数列![]() 满足:若
满足:若![]() 是数列
是数列![]() 中的一项,则
中的一项,则![]() 也是数列
也是数列![]() 中的一项,称数列
中的一项,称数列![]() 为“兑换数列”,常数
为“兑换数列”,常数![]() 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列:![]()
![]() 是“兑换系数”为
是“兑换系数”为![]() 的“兑换数列”,求
的“兑换数列”,求![]() 和
和![]() 的值;
的值;
(2)已知有穷等差数列![]() 的项数是
的项数是![]()
![]() ,所有项之和是
,所有项之和是![]() ,求证:数列
,求证:数列![]() 是“兑换数列”,并用
是“兑换数列”,并用![]() 和
和![]() 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不小于3项,且各项皆为正整数的递增数列![]() ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com