【题目】设为给定的不小于的正整数，考察个不同的正整数，，，构成的集合，若集合的任何两个不同的非空子集所含元素的总和均不相等，则称集合为“差异集合”．

（1）分别判断集合，集合是否是“差异集合”；（只需写出结论）

（2）设集合是“差异集合”，记，求证：数列的前项和；

（3）设集合是“差异集合”，求的最大值．

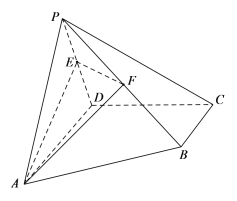
【题目】如图，在四棱锥中，平面，△为等边三角形，，，，分别为棱，的中点．

（1）求证：平面；

（2）求平面与平面所成锐二面角的余弦值；

（3）在棱上是否存在点，使得平面？若存在，求的值，若不存在，说明理由．

【题目】某贫困县在政府“精准扶贫”的政策指引下，充分利用自身资源，大力发展养茶业．该县农科所为了对比A，B两种不同品种茶叶的产量，在试验田上分别种植了A，B两种茶叶各亩，所得亩产数据（单位：千克）如下：

A：，，，，，，，，，，，，，，，，，，，；

B：，，，，，，，，，，，，，，，，，，，；

（1）从A，B两种茶叶亩产数据中各任取1个，求这两个数据都不低于的概率；

（2）从B品种茶叶的亩产数据中任取个，记这两个数据中不低于的个数为，求的分布列及数学期望；

（3）根据以上数据，你认为选择该县应种植茶叶A还是茶叶B？说明理由．

表1 田径综合赛项目及积分规则

表2 某队模拟成绩明细

根据模拟成绩，该代表队应选派参赛的队员是：（ ）

A.甲B.乙C.丙D.丁

【题目】如图，在正方体中，为棱的中点，动点在平面及其边界上运动，总有，则动点的轨迹为（ ）

A.两个点B.线段C.圆的一部分D.抛物线的一部分

【题目】已知数列中，已知，对任意都成立，数列的前n项和为．

（1）若是等差数列，求k的值；

（2）若，，求；

（3）是否存在实数k，使数列是公比不为1的等比数列，且任意相邻三项，，按某顺序排列后成等差数列？若存在，求出所有k的值；若不存在，请说明理由．

【题目】对于定义域为的函数，如果存在区间，其中，同时满足：

①在内是单调函数：②当定义域为时，的值域为，则称函数是区间上的“保值函数”，区间称为“保值函数”.

（1）求证：函数不是定义域上的“保值函数”；

（2）若函数（）是区间上的“保值函数”，求的取值范围；

（3）对（2）中函数，若不等式对恒成立，求实数的取值范围.

【题目】已知抛物线（），其准线方程，直线过点（），且与抛物线交于、两点，为坐标原点.

（1）求抛物线方程，并注明：的值与直线倾斜角的大小无关；

（2）若为抛物线上的动点，记的最小值为函数，求的解析式.

【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室，地面形状如图所示，已知已有两面墙的夹角为，墙的长度为米，（已有两面墙的可利用长度足够大），记.

（1）若，求的周长（结果精确到0.01米）；

（2）为了使小动物能健康成长，要求所建的三角形露天活动室面积，的面积尽可能大，当为何值时，该活动室面积最大？并求出最大面积.

【题目】如图，在正方体中， 分别是线段的中点．

（1）求异面直线与所成角的大小；

（2）求直线与平面所成角的大小．