
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的左右焦点,过点
分别是椭圆的左右焦点,过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,且
两点,且![]() 的周长为12.
的周长为12.
(Ⅰ)求椭圆![]() 的方程
的方程
(Ⅱ)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形若存在,求点
为底边的等腰三角形若存在,求点![]() 横坐标的取值范围,若不存在,请说明理由.
横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】高铁、移动支付、网购与共享单车被称为中国的新四大发明,为了解永安共享单车在淮南市的使用情况,永安公司调查了100辆共享单车每天使用时间的情况,得到了如图所示的频率分布直方图.
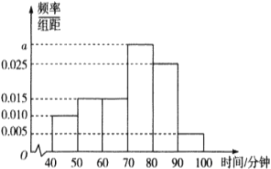
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现在用分层抽样的方法从前3组中随机抽取8辆永安共享单车,将该样本看成一个总体,从中随机抽取2辆,求其中恰有1辆的使用时间不低于50分钟的概率;
(Ⅲ)为进一步了解淮南市对永安共享单车的使用情况,永安公司随机抽取了200人进行调查问卷分析,得到如下2×2列联表:
经常使用 | 偶尔使用或不用 | 合计 | |
男性 | 50 | 100 | |
女性 | 40 | ||
合计 | 200 |
完成上述2×2列联表,并根据表中的数据判断是否有85%的把握认为淮南市使用永安共享单车的情况与性别有关?
附: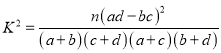
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 表示不小于
表示不小于![]() 的最小整数,例如
的最小整数,例如![]() .
.
(1)设![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 在区间
在区间![]()
![]() 上的值域为
上的值域为![]() ,集合
,集合![]() 中元素的个数为
中元素的个数为![]() ,求证:
,求证:![]() ;
;
(3)设![]() (
(![]() ),
),![]() ,若对于
,若对于![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 为抛物线
为抛物线![]() 上的点,若直线
上的点,若直线![]() 经过点
经过点![]() 且斜率为
且斜率为![]() ,则称直线
,则称直线![]() 为点
为点![]() 的“特征直线”.设
的“特征直线”.设![]() 、
、![]() 为方程
为方程![]() (
(![]() )的两个实根,记
)的两个实根,记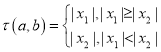 .
.
(1)求点![]() 的“特征直线”
的“特征直线”![]() 的方程;
的方程;
(2)已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 的“特征直线”与双曲线
的“特征直线”与双曲线![]() 经过二、四象限的渐进线垂直,且与
经过二、四象限的渐进线垂直,且与![]() 轴的交于点
轴的交于点![]() ,点
,点![]() 为线段
为线段![]() 上的点.求证:
上的点.求证:![]() ;
;
(3)已知![]() 、
、![]() 是抛物线
是抛物线![]() 上异于原点的两个不同的点,点
上异于原点的两个不同的点,点![]() 、
、![]() 的“特征直线”分别为
的“特征直线”分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且与
,且与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .求证:点
.求证:点![]() 在线段
在线段![]() 上的充要条件为
上的充要条件为![]() (其中
(其中![]() 为点
为点![]() 的横坐标).
的横坐标).
查看答案和解析>>
科目: 来源: 题型:
【题目】记点![]() 到图形
到图形![]() 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点![]() 到图形
到图形![]() 的距离,那么平面内到定圆
的距离,那么平面内到定圆![]() 的距离与到定点
的距离与到定点![]() 的距离相等的点的轨迹不可能是 ( )
的距离相等的点的轨迹不可能是 ( )
A.圆B.椭圆C.双曲线的一支D.直线
查看答案和解析>>
科目: 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且![]() (nN*).
(nN*).
(1)求{an}的通项公式;
(2)设数列![]() 满足
满足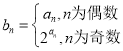 ,Tn为数列{bn}的前n项和,求Tn;
,Tn为数列{bn}的前n项和,求Tn;
(3)设![]() *(
*(![]() 为正整数),问是否存在正整数
为正整数),问是否存在正整数![]() ,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数
,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知椭圆![]() ,设
,设![]() 是椭圆
是椭圆![]() 上任一点,从原点
上任一点,从原点![]() 向圆
向圆![]() 作两条切线,切点分别为
作两条切线,切点分别为![]() .
.
(1)若直线![]() 互相垂直,且点
互相垂直,且点![]() 在第一象限内,求点
在第一象限内,求点![]() 的坐标;
的坐标;
(2)若直线![]() 的斜率都存在,并记为
的斜率都存在,并记为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA1→A1D1→ ,黄“电子狗”爬行的路线是AB→BB1→ ,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com