
科目: 来源: 题型:
【题目】公元前![]() 世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合
世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合![]() 中随机抽取两个数,则这两个数中有完全数的概率是______.
中随机抽取两个数,则这两个数中有完全数的概率是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,且
,且![]() .点
.点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
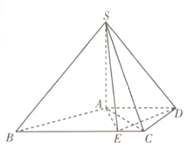
(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校的![]() 名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取
名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取![]() 名学生的数学成绩(满分:
名学生的数学成绩(满分:![]() 分),并绘制成如图所示的茎叶图.将成绩低于
分),并绘制成如图所示的茎叶图.将成绩低于![]() 分的称为“不及格”,不低于
分的称为“不及格”,不低于![]() 分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
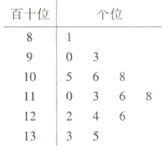
(1)估算此次联考该校高三学生的数学学科的平均成绩.
(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.
(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为![]() ;老师集中辅导的转化率为
;老师集中辅导的转化率为![]() ,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
注:转化率![]()
![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】公元前![]() 世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合
世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合![]() 中随机抽取两个数,则这两个数中有完全数的概率是______.
中随机抽取两个数,则这两个数中有完全数的概率是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com