
2009届高考数学第三轮复习精编模拟七
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、若sin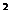 x>cos
x>cos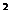 x,则x的取值范围是(
)w.w.w.k.s.5.u.c.o.m
x,则x的取值范围是(
)w.w.w.k.s.5.u.c.o.m
(A){x|2k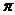 -
-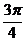 <x<2k
<x<2k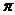 +
+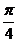 ,k
,k Z} (B) {x|2k
Z} (B) {x|2k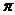 +
+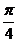 <x<2k
<x<2k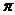 +
+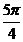 ,k
,k Z}
Z}
(C) {x|k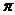 -
-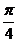 <x<k
<x<k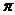 +
+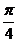 ,k
,k Z } (D) {x|k
Z } (D) {x|k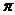 +
+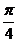 <x<k
<x<k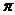 +
+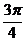 ,k
,k Z}
Z}
2 在复平面内,把复数3-
在复平面内,把复数3-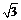 i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是…………………………( )w.w.w.k.s.5.u.c.o.m
i对应的向量按顺时针方向旋转π/3,所得向量对应的复数是…………………………( )w.w.w.k.s.5.u.c.o.m
 A)2
A)2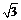 B)-2
B)-2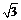 i C)
i C)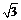 -3i D)3+
-3i D)3+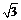 i
i
3、已知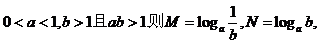
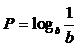 .三数大小关系为 ( )
.三数大小关系为 ( )
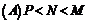
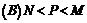
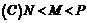
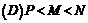
4、若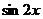 、
、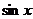 分别是
分别是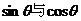 的等差中项和等比中项,则
的等差中项和等比中项,则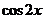 的值为:( )
的值为:( )
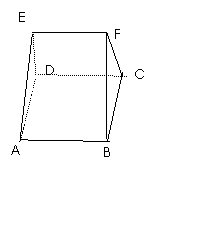 A、
A、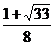 B、
B、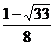 C、
C、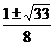 D、
D、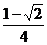
5、方程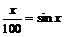 的实数解的个数为 ( )
的实数解的个数为 ( )
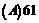
6、如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,
EF//AB, EF=3/2,EF与面AC的距离为2,则该多面体的体积为……( )
A)9/2 B)
7、过抛物线y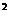 =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是(
)
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是(
)
(A) y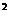 =2x-1
(B) y
=2x-1
(B) y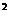 =2x-2
=2x-2
(C) y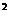 =-2x+1
(D) y
=-2x+1
(D) y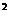 =-2x+2
=-2x+2
8、设函数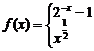
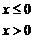 ,若
,若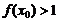 ,则
,则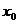 的取值范围是(
)
的取值范围是(
)
(A)(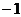 ,1)
(B)(
,1)
(B)(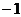 ,
,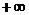 )
)
(C)(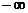 ,
,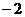 )
)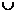 (0,
(0,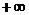 ) (D)(
) (D)(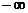 ,
,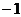 )
)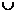 (1,
(1,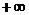 )
)
9、若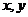 满足
满足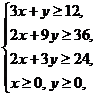 ,则使得
,则使得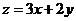 的值最小的
的值最小的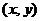 是 ( )
是 ( )
A、(4.5,3) B、(3,6) C、(9,2) D、(6,4)
10、已知两点M(1,5/4),N(-4,-5/4),给出下列曲线方程:
①4x+2y-1=0 ②x2+y2=3 ③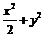 =1 ④
=1 ④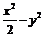 =1
=1
在曲线上存在点P满足|MP|=|NP|的所有曲线方程是………………………………( )
A)①③ B)②④ C)①②③ D)②③④
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、现时盛行的足球彩票,其规则如下:全部13场足球比赛,每场比赛有3种结果:胜、平、负,13长比赛全部猜中的为特等奖,仅猜中12场为一等奖,其它不设奖,则某人获得特等奖的概率为 。
12、数列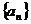 中,
中,
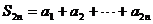 , 则
, 则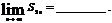
13、一只酒杯的轴截面是抛物线的一部分,它的函数解析式是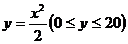 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
14、(坐标系与参数方程选做题)
已知圆的极坐标方程为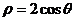 ,则该圆的圆心到直线
,则该圆的圆心到直线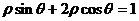 的距离是
.
的距离是
.
15.(几何证明选讲选做题) 已知AB是圆O的直径,EF切圆O于C,AD⊥EF于D,AD=2,AB=6,则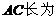 _______.
_______.
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知 ,
,
(Ⅰ)求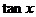 的值;
(Ⅱ)求
的值;
(Ⅱ)求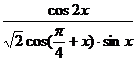 的值.
的值.
17. (本小题满分12分)
已知函数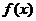 是定义在
是定义在 上的单调奇函数, 且
上的单调奇函数, 且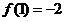 .
.
(Ⅰ)求证函数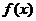 为
为 上的单调减函数;
上的单调减函数;
(Ⅱ) 解不等式 .
.
18.(本小题满分14分)
已知函数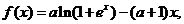 (其中
(其中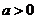 ) ,
) ,
点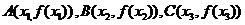 从左到右依次是函数
从左到右依次是函数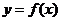 图象上三点,且
图象上三点,且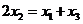 .
.
(Ⅰ) 证明: 函数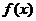 在
在 上是减函数;
上是减函数;
(Ⅱ)
求证:ㄓ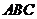 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,ㄓ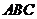 能否是等腰三角形?若能,求ㄓ
能否是等腰三角形?若能,求ㄓ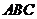 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
19.(本小题满分14分)
已知数列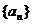 满足:
满足: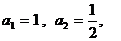 且
且
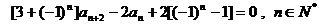 .
.
(Ⅰ)求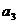 ,
,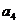 ,
,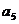 ,
,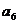 的值及数列
的值及数列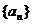 的通项公式;
的通项公式;
(Ⅱ)设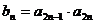 ,求数列
,求数列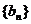 的前
的前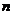 项和
项和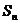 ;
;
20.(本小题满分14分)
(I)求证: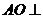 平面BCD;
平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A―CD―B的余弦值。
21. (本小题满分14分)
设直线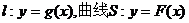 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有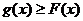 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数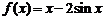 .求证:
.求证: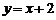 为曲线
为曲线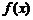 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
根据上图,试推测曲线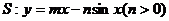 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
一.选择题:DBBAC DBDBD
解析:1:由sin x>cos
x>cos x得cos
x得cos x-sin
x-sin x<0, 即cos2x<0,所以:
x<0, 即cos2x<0,所以: +kπ<2x<
+kπ<2x< +kπ,选D.
+kπ,选D.
2:∵复数3- i的一个辐角为-π/6,对应的向量按顺时针方向旋转π/3,
i的一个辐角为-π/6,对应的向量按顺时针方向旋转π/3,
所得向量对应的辐角为-π/2,此时复数应为纯虚数,对照各选择项,选(B)。
3:由 又
又 代入选择支检验
代入选择支检验 被排除;又由
被排除;又由 ,
, 即
即 被排除.故选
被排除.故选 .
.
4:依题意有 , ①
, ①  ②
②
由①2-②×2得, ,解得
,解得 。
。
又由 ,得
,得 ,所以
,所以 不合题意。故选A。
不合题意。故选A。
5:令 ,这两个方程的曲线交点的个数就是原方程实数解的个数.由于直线
,这两个方程的曲线交点的个数就是原方程实数解的个数.由于直线 的斜率为
的斜率为 ,又
,又 所以仅当
所以仅当 时,两图象有交点.由函数
时,两图象有交点.由函数 的周期性,把闭区间
的周期性,把闭区间 分成
分成


 共
共 个区间,在每个区间上,两图象都有两个交点,注意到原点多计一次,故实际交点有
个区间,在每个区间上,两图象都有两个交点,注意到原点多计一次,故实际交点有 个.即原方程有63个实数解.故选
个.即原方程有63个实数解.故选 .
.
6:连接BE、CE则四棱锥E-ABCD的体积VE-ABCD= ×3×3×2=6,又整个几何体大于部分的体积,所求几何体的体积V求> VE-ABCD,选(D)
×3×3×2=6,又整个几何体大于部分的体积,所求几何体的体积V求> VE-ABCD,选(D)
|