|
试题详情
试题详情
(8) 是直线 是直线 垂直的( ) 垂直的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 试题详情
试题详情
A. B. B. C. C. D. D. (10)椭圆C1:+=1的左准线为l,左、右焦点分别为F1、F2,抛物线C2的准线也是l,焦点为F2,C1与C2的一个交点为P,则|PF2|的值等于 A. B. C.2 D. 试题详情
试题详情
试题详情
(文)使 成立的 成立的 的一个区间是( ) 的一个区间是( ) 试题详情
试题详情
(12)定义在R上的函数f (x)满足f (4)=1. f ′(x)为f(x)的导函数,已知函数y =
f ′(x)的图象如下图所示.若两正数a, b满足f
(2a+b)<1, 则 的取值范围是 的取值范围是 试题详情
试题详情
C. D. D. 第Ⅱ卷(非选择题
共90分) 试题详情
注意事项: 请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效. 试题详情
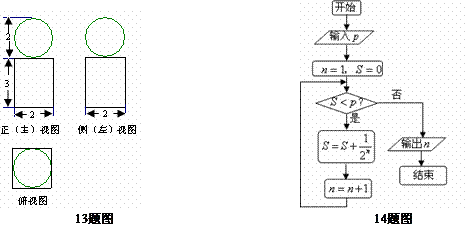
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.  (13)如图是一个几何体的三视图,则这个几何体的表面积和体积分别为 ; (13)如图是一个几何体的三视图,则这个几何体的表面积和体积分别为 ;
试题详情
(14)执行下面的程序框图,若 ,则输出的 ,则输出的 ; ; 试题详情
(15)当 时,函数 时,函数 的最小值为 ; 的最小值为 ; 试题详情
(16)给出下列4个命题: 试题详情
试题详情
试题详情
试题详情
④在 中,若 中,若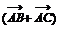  ,则 ,则 为等腰三角形. 为等腰三角形. 其中正确的命题是 . (注:把你认为正确的命题的序号都填上.) (17)(本小题满分12分) 试题详情
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
试题详情
Ⅰ)求 的值; 的值; 试题详情
(Ⅱ)将函数 的图象向右平移 的图象向右平移 个单位后,得到函数 个单位后,得到函数 的图象,求 的图象,求 的单调递减区间. 的单调递减区间. (18(本小题满分12分) 试题详情
试题详情
试题详情
(Ⅱ)要使10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益,求 的取值范围. 的取值范围. 试题详情
(文科做) 为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体. (Ⅰ)求该总体的平均数; 试题详情
(Ⅱ)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率. 试题详情
(19)(本小题满分13分) (理)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, AB=,AF=1,M是线段EF的中点. (Ⅰ)求证AM∥平面BDE; (Ⅱ)求二面角A-DF-B的大小; (Ⅲ)试在线段AC上确定一点P,使得PF与CD所成的角是60°. 试题详情
试题详情
(文)如图,ABCD、CDEF是两个边长都为 的正方形, 的正方形, 且平面ABCD⊥平面CDEF,M、N分别是AB、AC的中点, H是DE上的一个动点。 (Ⅰ)求证:HN⊥AC; (Ⅱ)当EH=HD时,在AD上确定一点P,使得HP∥平面EMC. (20)(本小题满分12分) 试题详情
已知 . . 试题详情
试题详情
(Ⅱ)若 在 在 内有且只有一个极值点, 求 内有且只有一个极值点, 求 的取值范围. 的取值范围. (21)(本小题满分12分) 试题详情
试题详情
(Ⅰ)证明数列 是等比数列; 是等比数列; 试题详情
试题详情
(Ⅲ)证明不等式 ,对任意 ,对任意 皆成立. 皆成立. 试题详情
试题详情
(Ⅱ)如果椭圆上的两点P,Q使 的平分线垂直于OA,是否总存在实数 的平分线垂直于OA,是否总存在实数 ,使得 ,使得 ?请说明理由. ?请说明理由. 2009届马鞍山市高三期未考试试卷 数学参考解答及评分标准 第I卷(选择题,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C C B C A C A D D D/A C 第Ⅱ卷(非选择题
共95分) 试题详情
二、填空题 (13) ; (14) 4; (15)3 ; 16)①③④. ; (14) 4; (15)3 ; 16)①③④. 试题详情
试题详情
 .………………………………………………………………………2分 .………………………………………………………………………2分
试题详情
试题详情
因此 . . 试题详情
即 , , 试题详情
试题详情
试题详情
试题详情
因此 . ……………………………………………………………7分 . ……………………………………………………………7分 试题详情
试题详情
所以 .……………………9分 .……………………9分 试题详情
当 ( ( ),……10分 ),……10分 试题详情
试题详情
试题详情
18(理科做) 解:(Ⅰ)依题意,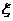 可能的取值为1,0, 可能的取值为1,0,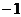 . ……………………2分 . ……………………2分 试题详情
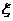 的分布列为(列出下表得3分)……………………………………………………5分 的分布列为(列出下表得3分)……………………………………………………5分
试题详情
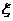
1 0 试题详情
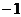
P 试题详情
试题详情
试题详情
试题详情
 = = .…………………………………………………………………6分 .…………………………………………………………………6分
试题详情
(Ⅱ)设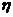 表示10万元投资乙项目的收益,则 表示10万元投资乙项目的收益,则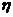 的分布列为(列出下表得2分)…8分 的分布列为(列出下表得2分)…8分 试题详情
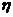
2 试题详情
P 试题详情
试题详情
试题详情
 . ………………………10分 . ………………………10分
试题详情
依题意要求 ≥ ≥ ,……………………11分 ,……………………11分 试题详情
∴ ≤ ≤ ≤1. ……………………………12分 ≤1. ……………………………12分 (文)(Ⅰ)总体平均数为 试题详情
 .??????????????????????? 4分 .??????????????????????? 4分
试题详情
(Ⅱ)设 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”. 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”. 试题详情
试题详情
试题详情
所以所求的概率为 .………………………………………………………………12分 .………………………………………………………………12分 试题详情
19.(理)解:(Ⅰ)如图建立空间直角坐标系,设AC∩BD=N,连结NE, 则、E(0,0,1),∴=. 试题详情
 又、,∴ 又、,∴
∴,又NE与AM不共线,∴NE∥AM. ……………………3分 试题详情
又NE 平面BDE且AM 平面BDE且AM 平面BDE,∴AM∥平面BDE. ………4分 平面BDE,∴AM∥平面BDE. ………4分 (Ⅱ)∵AF⊥AB,AB⊥AD,AF∩AD=A,∴AB⊥平面ADF, ∴=(,0,0)为平面DAF的法向量. …………………5分 又∵=?=0,
=?=0, ∴NE⊥DB,NE⊥NF,∴NE⊥平面BDF,即为平面BDF的法向量. …………6分 试题详情
又∵cos〈〉= =,∴的夹角为60°…8分 =,∴的夹角为60°…8分 又由图可判定二面角A-DF-B的大小为锐角, ∴所求二面角A-DF-B的大小为60°. …………………………………………………9分 (Ⅲ)设P(t,t,0)(0≤t≤),则=,=. ∵与CD所成的角为60°,∴,……………………11分 解之得(舍去), 故点P为AC的中点. ………………………………………………12分 试题详情
19.(文)解: (Ⅰ)证明:连接BD、BE, 由ABCD是正方形,得AC⊥BD…………①,且交于N, 因为平面ABCD⊥平面CDEF,交线为CD,ED⊥CD,故ED⊥平面ABCD,…………4分 所以ED⊥AC…………②,又ED∩BD=D………③, 由①②③知,AC⊥平面BDE 试题详情
HN 平面BDE,故HN⊥AC ………………………………………………………………6分 平面BDE,故HN⊥AC ………………………………………………………………6分 试题详情
 (Ⅱ) EH=HD时,H为DE的中点,取CD中点S, (Ⅱ) EH=HD时,H为DE的中点,取CD中点S,
连接HS、AH、AS, 则有HS∥EC、AS∥MC,又HS∩AS=S,CE∩MC=C, 故平面MCE∥平面ASH………………………10分 试题详情
又AH 平面ASH,所以AH∥平面MCE, 平面ASH,所以AH∥平面MCE, 又A在AD上,故点A为符合条件的点,即P在A处. …12分 试题详情
20,(Ⅰ) ∵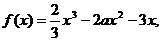 试题详情
∴ ……………………………………………………………1分 ……………………………………………………………1分 试题详情
∵ , ∴ , ∴ …………………………………………………………3分 …………………………………………………………3分 试题详情
又∵二次函数 的图象开口向上, 的图象开口向上, 试题详情
∴在 内 内 , ………………………………………………………………………5分 , ………………………………………………………………………5分 试题详情
故 在 在 内是减函数. …………………………………………………………………6分 内是减函数. …………………………………………………………………6分 试题详情
试题详情
试题详情
当 时, ∵ 时, ∵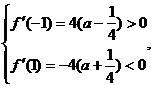 试题详情
试题详情
试题详情
试题详情
试题详情
故所求 的取值范围为 的取值范围为 …………………………………………12分 …………………………………………12分 试题详情
试题详情
试题详情
试题详情
试题详情
(Ⅲ)证明:对任意的 , , 试题详情
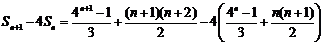  . .
试题详情
所以不等式 ,对任意 ,对任意 皆成立…………………………………………12分. 皆成立…………………………………………12分. 试题详情
22(Ⅰ)由题意知: , , , , 试题详情
则椭圆方程为 …………………………………………………………………………2分 …………………………………………………………………………2分 试题详情
由椭圆的对称性知: , , 试题详情
试题详情
试题详情
即椭圆方程为 ;………………………………………………………………6分 ;………………………………………………………………6分 试题详情
试题详情
试题详情
若设CP: ,则CQ: ,则CQ: , , 试题详情
由 ,………………9分 ,………………9分 试题详情
试题详情
试题详情
故 ,故 ,故 , ………………13分 , ………………13分 试题详情
即总存在实数 ,使得 ,使得 …………………………………………14分 …………………………………………14分 试题详情
| 


 其中R表示球的半径
其中R表示球的半径 ,且
,且 的集合
的集合 的个数是( )
的个数是( ) 在复平面内对应的点位于
在复平面内对应的点位于 是幂函数,则函数
是幂函数,则函数 的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( ) (4)右图是根据《安徽统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )
(4)右图是根据《安徽统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( ) 展开式中的常数项为( )
展开式中的常数项为( ) B.1320 C.
B.1320 C. D.220
D.220 ,则不等式
,则不等式 的解集为
的解集为 B.
B. C.
C.  D.
D.
 }是等差数列,
}是等差数列, ,
, ,则过点
,则过点 ,
,