
科目:gzsx 来源: 题型:
| a |
| x |
| g(x) |
| x2 |
科目:gzsx 来源: 题型:
| a |
| x |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| lnx |
| x |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| a |
| x |
| 3 |
| 2 |
科目:gzsx 来源: 题型:
| a | x |
科目:gzsx 来源: 题型:
| a |
| x |
|
科目:gzsx 来源: 题型:
| b |
| x |
| a |
| e |
科目:gzsx 来源: 题型:
| mx |
| x2+n |
| a |
| x |
| 7 |
| 2 |
科目:gzsx 来源: 题型:
| a |
| x |
| 1 |
| e |
| n |
| n-1 |
| 1 |
| n |
科目:gzsx 来源: 题型:
| 1 |
| x |
| a |
| x |
科目:gzsx 来源: 题型:
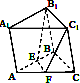 给出下列命题:
给出下列命题:| 1 |
| 2x-1 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| a | x |
科目:gzsx 来源: 题型:
| a |
| x |
| 5 |
| 2 |
科目:gzsx 来源: 题型:
| a |
| x |
|
科目:gzsx 来源: 题型:
| a |
| x |
| 2 |
| π |
| 4 |
| 22+22 |
| 2 |
科目:gzsx 来源: 题型:
| 1 | 2 |
科目:gzsx 来源: 题型:
| 1 |
| x |
| 2 |
| e |
科目:gzsx 来源: 题型:
| a |
| x |
| 3 |
| 2 |