已知f(x2-1)定义域为[-2,2],求f(x)的定义域答案解析
科目:gzsx
来源:
题型:
已知函数f(x)=lnx+x2
(1)若函数g(x)=f(x)-ax在其定义域内为增函数,求实数a的取值范围.
(2)在(1)条件下若a>1,h(x)=x3-3ax,x∈[1,2],求h(x)的最小值;
(3)设F(x)=2f(x)-3x2-kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n)且2x0=m+n,证明:函数F(x)在点(x0,f(x0))处的切线不可能平行于x轴.
查看答案和解析>>
科目:gzsx
来源:2011年山东省潍坊市高考数学一模试卷(文科)(解析版)
题型:解答题
已知函数f(x)=lnx+x2
(1)若函数g(x)=f(x)-ax在其定义域内为增函数,求实数a的取值范围.
(2)在(1)条件下若a>1,h(x)=x3-3ax,x∈[1,2],求h(x)的最小值;
(3)设F(x)=2f(x)-3x2-kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n)且2x=m+n,证明:函数F(x)在点(x,f(x))处的切线不可能平行于x轴.
查看答案和解析>>
科目:gzsx
来源:山东省模拟题
题型:解答题
已知函数f(x)=lnx+x2。
(1)若函数g(x)=f(x)-ax在其定义域内为增函数,求实数a的取值范围;
(2)在(1)的条件下,若a>1,h(x)=x3-3ax,x∈[1,2],求h(x)的极小值;
(3)设F(x)=2f(x)-3x2-kx(k∈R),若函数F(x)存在两个零点,m,n(0<m<n),且2x0=m+n,证明:函数F(x)在点(x0,F(x0))处的切线不可能平行于x轴。
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•杨浦区二模)(理)已知向量
=(x2+1,-x),
=(1,2) (n为正整数),函数
f(x)=• ,设f(x)在(0,+∞)上取最小值时的自变量x取值为a
n.
(1)求数列{a
n}的通项公式;
(2)已知数列{b
n},对任意正整数n,都有b
n•(4a
n2-5)=1成立,设S
n为数列{b
n}的前n项和,求
Sn;
(3)在点列A
1(1,a
1)、A
2(2,a
2)、A
3(3,a
3)、…、A
n(n,a
n)、…中是否存在两点A
i,A
j(i,j为正整数)使直线A
iA
j的斜率为1?若存在,则求出所有的数对(i,j);若不存在,请你写出理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=3x,且f-1(18)=a+2,g(x)=3ax-4x的定义域为[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其单调性并用定义证明;
(3)求g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•杨浦区二模)(文)已知向量
=(x2+1,-x),
=(1,2) (n为正整数),函数
f(x)=• ,设f(x)在(0,+∞)上取最小值时的自变量x取值为a
n.
(1)求数列{a
n}的通项公式;
(2)已知数列{b
n},其中b
n=a
n+12-a
n2,设S
n为数列{b
n}的前n项和,求
;
(3)已知点列A
1(1,a
12)、A
2(2,a
22)、A
3(3,a
32)、…、A
n(n,a
n2)、…,设过任意两点A
i,A
j(i,j为正整数)的直线斜率为k
ij,当i=2008,j=2010时,求直线A
iA
j的斜率.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=xlnx,g(x)=f(x)+f(m-x),m为正的常数.
(1)求函数g(x)的定义域;
(2)求g(x)的单调区间,并指明单调性;
(3)若a>0,b>0,证明:f(a)+(a+b)ln2≥f(a+b)-f(b).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-2,2].
(1)求g(x)的解析式;
(2)求g(x)的单调区间;
(3)求g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x
2-kx
3.(k≥0)
(Ⅰ)求g(x)的解析式;
(Ⅱ)讨论函数f(x)在区间(-∞,0)上的单调性;
(Ⅲ)若
k=,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
[,a]上的值域为
[,1],若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•杭州二模)已知椭圆
+=1 (a > b > 0)上任一点P到两个焦点的距离的和为
2,P与椭圆长轴两顶点连线的斜率之积为
-.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x
1,y
1),B(x
2,y
2).
(Ⅰ)若
•=(O为坐标原点),求|y
1-y
2|的值;
(Ⅱ)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA、QB的倾斜 角互为补角?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知
f(x)=ax3-a2x,f(x)的定义域为R,函数
g(x)=,g(x)的定义域为[0,2].
(1)设a≠0,求f(x)的单调区间;
(2)求g(x)的值域;
(3)设a>0,若对任意x
1∈[0,2],总存在x
0∈[0,2],使g(x
1)-f(x
0)=0,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数
y=,若f( x
o)=5,则 x
o的值是
-2
-2
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=log2x+3,x∈[1,4]
(1)求函数f(x)的值域;
(2)若g(x)=f(x2)-[f(x)]2,求g(x)的最小值以及相应的x的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数f(x)=ka
x-a
-x(a>0且a≠1,k∈R),f(x)是定义域为R上的奇函数.
(1)求k的值,并证明当a>1时,函数f(x)是R上的增函数;
(2)已知
f(1)=,函数g(x)=a
2x+a
-2x-4f(x),x∈[1,2],求g(x)的值域;
(3)若a=4,试问是否存在正整数λ,使得f(2x)≥λ•f(x)对
x∈[-,]恒成立?若存在,请求出所有的正整数λ;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=x+
…+
,g(x)=
+
…+
,定义域为R,m,n∈N
•,h
1(x)=c+f(x)-g(x),h
2(x)=c-f(x)+g(x)
(1)若n=1,m=2,求h
1(x)的单调区间;若n=2,m=2,求h
2(x)的最小值.
(2)(文科选做)若m=n,c=0时,令T(n)=h
2(1),求T(n)的最大值.
(理科选做)若m=n,c=0时,令T(n)=h
1(1),求证:T(n)=
+
+…+
.
(3)若m=n+1,c=1时,F(x)=h
1(x+3)h
2(x-2)且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,求b-a的最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数f(x),g(x)满足关系g(x)=f(x)•f(x+α)其中α是常数.
(1)设f(x)=cosx+sinx,α=
,求g(x)的解析式;
(2)设计一个函数f(x)及一个α(0<α<π)的值使得g(x)=
sin2x;
(3)设常数α=0,f(x)=
(0<k<1),并已知0<x
1<x
2<
时,总有
>成立,当
x∈( 0,)时,试比较sin[g(x)]与g(sinx)的大小.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知f(x)=3x且f(a+2)=18,g(x)=3ax-4x的定义域为[0,1].
(1)求g(x)的解析式;
(2)求g(x)的值域.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知
=(x
2+1,p+2),
=(3,x),f(x)=
•,P是实数.
(1)若存在唯一实数x,使
+
与
=(1,2)平行,试求P的值;
(2)若函数y=f(x)是偶函数,试求y=|f(x)-15|在区间[-1,3]上的值域.
查看答案和解析>>
科目:gzsx
来源:2011年高三数学第一轮基础知识训练(20)(解析版)
题型:解答题
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x
2-kx
3.(k≥0)
(Ⅰ)求g(x)的解析式;
(Ⅱ)讨论函数f(x)在区间(-∞,0)上的单调性;
(Ⅲ)若
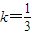
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
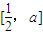
上的值域为
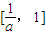
,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>

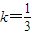 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间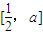 上的值域为
上的值域为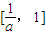 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.