如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和答案解析
科目:czsx
来源:新课标3维同步训练与评价数学 九年级(下)
题型:044
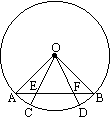
如图,在⊙O中,AB与OC,OD分别交于E,F,且AE=BF,那么
(1)OE与OF有什么关系?为什么?
(2) 与
与 相等吗?为什么?
相等吗?为什么?
查看答案和解析>>
科目:czsx
来源:
题型:
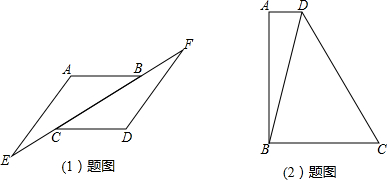
(2013•历下区二模)(1)如图1,AB∥CD,AB=CD,直线EF分别交AB、CD 于B、C,且BF=EC.求证:∠A=∠D.
(2)如图2,梯形ABCD中,AD∥BC,∠A=90°,BC=2,∠ABD=15°,∠C=60°.①求∠BDC的度数;②求AB的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
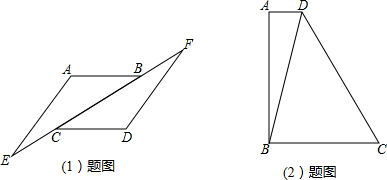
(1)如图1,AB∥CD,AB=CD,直线EF分别交AB、CD 于B、C,且BF=EC.求证:∠A=∠D.
(2)如图2,梯形ABCD中,AD∥BC,∠A=90°,BC=2,∠ABD=15°,∠C=60°.①求∠BDC的度数;②求AB的长.
查看答案和解析>>
科目:czsx
来源:2013年山东省济南市历下区中考数学二模试卷(解析版)
题型:解答题
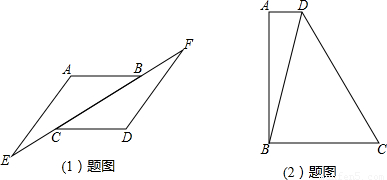
(1)如图1,AB∥CD,AB=CD,直线EF分别交AB、CD 于B、C,且BF=EC.求证:∠A=∠D.
(2)如图2,梯形ABCD中,AD∥BC,∠A=90°,BC=2,∠ABD=15°,∠C=60°.①求∠BDC的度数;②求AB的长.
查看答案和解析>>
科目:czsx
来源:
题型:013
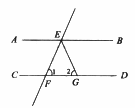
如图所示:已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为(
)
A
.50°
B.60°
C.65°
D.70°
查看答案和解析>>
科目:czsx
来源:1+1轻巧夺冠·优化训练(冀教版)七年级数学(下) 冀教版银版
题型:013
如图所示:已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为

[ ]
查看答案和解析>>
科目:czsx
来源:新教材完全解读 七年级数学 (下册) (配人教版新课标) (第1次修订版) 配人教版新课标
题型:013
如图所示,已知AB∥CD,直线EF分别交AB和CD于点E和F,EG平分∠BEF,若∠1=50°,则∠2的度数为

[ ]
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在▱ABCD中,E、F分别是AB、AD的中点,EF交AC于点G,则
的值是
.
查看答案和解析>>
科目:czsx
来源:
题型:
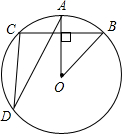
如图,在⊙O中,OA⊥BC,∠CDA=25°,则∠AOB的度数为( )
查看答案和解析>>
科目:czsx
来源:
题型:

23、如图,在▱ABCD中,M、N分别是AB、CD的中点,BD分别交AN、CM于点P、Q,
(1)求证:四边形AMCN是平行四边形;
(2)判断DP、PQ、QB的数量关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
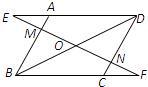
21、已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△
≌△
,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
查看答案和解析>>
科目:czsx
来源:
题型:
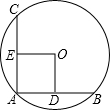
如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则⊙O的半径为
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在□ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF,点P为直线CD上一点(不与点C重合).
(1)在图1中画图探究:
当点P在CD延长线上时,连结EP并把EP绕点E逆时针旋转90°得到线段EQ.作直线QF交直线CD于H,求证:QF⊥CD.
(2)探究:结合(1)中的画图步骤,分析线段QH、PH与CE之间是否存在一种特定的数量关系?请在下面的空格中写出你的结论;若存在,直接填写这个关系式.
①当点P在CD延长线上且位于H点右边时,
QH-PH=2CE
QH-PH=2CE
;
②当点P在边CD上时,
QH+PH=2CE
QH+PH=2CE
.
(3)若AD=2AB=6,AE=1,连接DF,过P、F两点作⊙M,使⊙M同时与直线CD、DF相切,求⊙M的半径是多少?

查看答案和解析>>
科目:czsx
来源:
题型:
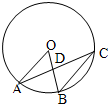
7、如图,在⊙O中,OA∥BC,∠B=40°,则∠OAC的度数是( )
查看答案和解析>>
科目:czsx
来源:
题型:
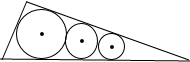
如图,在△OAB中放置了3个圆,它们与相邻的三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是
.
查看答案和解析>>
科目:czsx
来源:
题型:
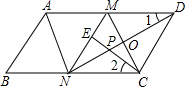
(2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:czsx
来源:
题型:
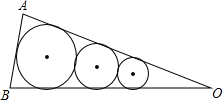
如图:在△OAB中放置了3个圆,它们与三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在⊙O中,
=,试比较AB与CD的长度,并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在⊙O中∠ACB=∠BDC=60°,
AC=2,则⊙O的周长是
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在▱ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,则DE的长为( )
查看答案和解析>>

![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?






 23、如图,在▱ABCD中,M、N分别是AB、CD的中点,BD分别交AN、CM于点P、Q,
23、如图,在▱ABCD中,M、N分别是AB、CD的中点,BD分别交AN、CM于点P、Q, 21、已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
21、已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
 (2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
(2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O. 如图:在△OAB中放置了3个圆,它们与三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是( )
如图:在△OAB中放置了3个圆,它们与三角形的边相切,与相邻的圆相外切,已知最大圆与最小圆的半径分别是4、2,那么中间的圆的半径是( )