科目：gzsx 来源：山东省潍坊市四县一校2012届高三上学期模块监测考试数学文科试题(人教版) 人教版 题型：044
已知函数f(x)＝2asinωxcosωx＋2
cos2ω－
(a、ω＞0)的最大值为2．
x1，x2是集合M＝{x∈R|f(x)＝0}中的任意两个元素，|x1－x2|的最小值为
．
(Ⅰ)求a、ω的值
(Ⅱ)若f(a)＝
，求sin(
－4α)的值．
科目：gzsx 来源：江西省六校2012届高三第一次联考数学文科试题 题型：044
已知函数f(x)＝sin(
)(
＞0，0≤
≤π)为偶函数，其图像上相邻的两个最高点间的距离为2π．
(Ⅰ)求f(x)的解析式；
(Ⅱ)若a∈(－
，
)，f(α，)＝
，求sin(2α＋
)的值．
科目：gzsx 来源：江西省会昌中学2011届高三第一次月考文科数学试题 题型：044
已知函数f(x)＝Asin(3x＋
)(A＞0，x∈(－∞，＋∞)，0＜＜π)在x＝
时取得最大值4．
(1)求f(x)的最小正周期；
(2)求f(x)的解析式；
(3)若f(
α＋
)＝
，求sinα．
科目：gzsx 来源：云南省武定县第一中学2011届高三8月月考文科数学试题 题型：044
设函数f(x)＝3sin(ωx＋
)，ω＞0，x∈(－∞，＋∞)，且以
为最小正周期．
(1)求f(0)；
(2)求f(x)的解析式；
(3)已知f(
＋
)＝
，求sinα的值．
科目：gzsx 来源：山东省潍坊市四县一校2012届高三上学期模块监测考试数学理科试题(人教版) 人教版 题型：044
已知函数f(x)＝2asinωxcosωx＋2
cos2ωx－
(a、ω＞0)的最大值为2．
x1，x2是集合M＝{x∈R|f(x)＝0}中的任意两个元素，|x1－x2|的最小值为
．
(Ⅰ)求a、ω的值
(Ⅱ)若f(a)＝
，求sin(
－6α)的值．
科目：gzsx 来源： 题型：
已知向量a＝(cos
x，sinx)，b＝(cos
，sin)，c＝(
，－1)，其中x∈R，
(1)当a·b＝
时，求x值的集合；
(2)设函数f(x)＝(a－c)2，求f(x)的最小正周期及其单调增区间.
科目：gzsx 来源：2011-2012学年湖北省八校高三第二次联考文科数学试卷（解析版） 题型：填空题
若函数f(x)=sinωx+
cosωx
满足f(α)＝－2，f(β)＝0，且｜α－β｜的最小值为
，则函数f(x)的单调增区间为_____________
科目：gzsx 来源：2015届江西省高一第一次月考数学试卷（解析版） 题型：选择题
定义在R上的函数f(x)满足f(x)＝f(x＋2)，当x∈[3,5]时，f(x)＝2－|x－4|，则( )
(A)f(sin
)<f(cos) (B)f(sin1)>f(cos1)
(C)f(cos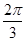
)<f(sin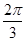) (D)f(cos2)>f(sin2)
科目：gzsx 来源：2010-2011学年江西师大附中高三理科数学月考试卷 题型：选择题
已知函数f(x)＝sin(x－)＋cos(x－)，g(x)＝f(－x)，直线x＝m与f(x)和g(x)的图象分别交于M，N两点，则|MN|的最大值为（ ）
A．4 B．3 C．2 D．1
科目：gzsx 来源：2011年吉林省高一上学期期末质量检测数学试卷 题型：填空题
给出下列五个命题：
①函数y＝tanx的图象关于点（kπ＋
，0）（k∈Z）对称；
②函数f (x)＝sin|x|是最小正周期为π的周期函数；
③函数y＝cos2x＋sinx的最小值为－1；
④设θ为第二象限的角，则tan
＞cos，且sin＞cos；
⑤若
．
其中正确的命题序号是________________________．；
科目：gzsx 来源：2014届山西省高一下学期月考数学试卷 题型：填空题
有下列命题：
①函数y＝cos（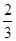
x+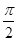
）是奇函数；
②函数f(x)＝4sin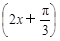
的表达式可改写为f(x)= 4cos
；
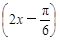③若α、β是第一象限角且α<β，则tan α<tan β；
④函数y＝sin（2x+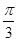
）的图象关于直线x=
成轴对称图形.
其中正确的是__________（把你认为正确的命题序号都填上）
科目：gzsx 来源：2014届浙江省杭州地区七校高一下学期期中联考数学试卷（解析版） 题型：解答题
设f (x)＝sin 2x＋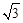
(sin
x－cos x)(sin x＋cos x)，其中x∈R．
(Ⅰ) 该函数的图象可由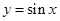
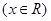的图象经过怎样的平移和伸缩变换得到？
(Ⅱ)若f (θ)＝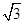
，其中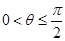
，求cos(θ＋
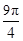)的值；
科目：gzsx 来源：2015届广东省高一下学期期中考试理科数学试卷（解析版） 题型：选择题
函数f(x)＝M sin (ωx＋φ)，(ω＞0) 在区间 [ a , b ] 上是增函数，且f(a)＝－M，f(b)＝M，则函数g(x)＝M cos (ωx＋φ) 在 [ a , b ] 上（ ）
A．增函数 B．是减函数 C．可以取最大值M D．可以取最小值－M
科目：gzsx 来源：2012-2013学年浙江省高三高考模拟测试理科数学试卷（解析版） 题型：解答题
已知函数f (x)＝3 sin2 ax＋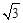
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
(Ⅰ) 求a的值；
(Ⅱ) 求f (x)的值域．
科目：gzsx 来源：2012年苏教版高中数学必修4 1.3三角函数的图象和性质练习卷（解析版） 题型：选择题
已知f(x)＝sin(x＋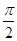
),g(x)＝cos(x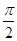－），则f(x)的图象
A.与g(x)的图象相同
B.与g(x)的图象关于y轴对称
C.向左平移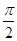个单位，得到g(x)的图象
D.向右平移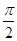个单位，得到g(x)的图象
科目：gzsx 来源： 题型：
已知函数f(x)＝
·
，其中＝(sinωx＋cosωx,
cosωx),＝cosωx－sinωx,2sinωx)(ω＞0)，若f(x)相邻的对称轴之间的距离不小于
.
(1)求ω的取值范围；
(2)在△ABC中，a,b,c分别为A,B,C的对边，a＝,b+c＝3，当ω最大时，f(A)＝1，求△ABC的面积.
科目：gzsx 来源：2013届浙江省高二下学期第一次质检理科数学试卷（解析版） 题型：选择题
若对可导函数f(x)，g(x)，当x∈[0,1]时恒有f′(x)·g(x)<f(x)·g′(x)，若已知α，β是一个锐角三角形的两个内角，且α≠β，记F(x)＝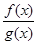
(g(x)≠0)，则下列不等式正确的是( )
A．F(cosα)>F(cosβ) B．F(cosα)<F(cosβ) C．F(sinα)<F(cosβ) D．F(sinα)>F(sinβ)
科目：gzsx 来源：2012-2013学年浙江省高三第一次月考理科数学试卷（解析版） 题型：填空题
给出定义：若函数f(x)在D上可导，即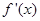
存在，且导函数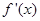在D上也可导，则称f(x)在D上存在二阶导函数，记
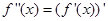，若
在D上恒成立，则称f(x)在D上为凸函数．以下四个函数在(0，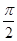
)上是凸函数的是_____
___．(把你认为正确的序号都填上)
① f(x)＝sin x＋cos x； ② f(x)＝ln x－2x；
③ f(x)＝－x3＋2x－1； ④ f(x)＝xex．
科目：gzsx 来源：2012年人教A版高中数学必修四1.5函数的图象练习卷（二）（解析版） 题型：选择题
已知函数f(x)＝cos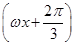
(x∈R，ω>0)的最小正周期为
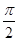，为了得到函数g(x)＝sinωx的图象，只要将y＝f(x)的图象( )
A．向左平移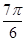
个单位长度
B．向右平移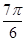个单位长度
C．向左平移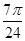
个单位长度
D．向右平移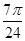个单位长度
＋
)，则f(1)＋f(2)＋f(3)＋…＋f(2004)＝________．