在直角坐标系中，C(2,3),C′(-4，3)，C″(2，1)答案解析

科目：czsx 来源： 题型：

在直角坐标系中，将坐标为（5，6），（1，2），（3，2），（3，0），（7，0），（7，2），（9，2），（5，6）的点用线段依此连接起来形成一个图案．
（1）纵坐标保持不变，横坐标分别减去3呢，与原图形相比，所得图形有什么变化？
（2）横坐标保持不变，纵坐标分别乘以-1，与原图形相比，所得图形有什么变化？
（3）横坐标加上2，纵坐标减去3呢，与原图形相比，所得图形有什么变化？

科目：czsx 来源： 题型：

如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标；
（2）求出S_△ABC；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化后的图形，并判断线段AB和线段A′B′的关系．

科目：czsx 来源： 题型：

如图，在直角坐标系中，A点、B点坐标分别为（2，0），（0，1），要使四边形BOAC为矩形，则C点坐标为

（2，1）

（2，1）

．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

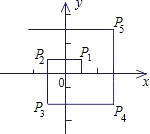
在直角坐标系中，设一质点M自P₀（1，0）处向上运动1个单位至P₁（1，1），然后向左运动2个单位至P₂处，再向下运动3个单位至P₃处，再向右运动4个单位至P₄处，再向上运动5个单位至P₅处，…如此继续运动下去，设P_n（x_n，y_n），n=1，2，3，…．
（1）依次写出x₁、x₂、x₃、x₄、x₅、x₆的值；
（2）计算x₁+x₂+…+x₈的值；
（3）计算x₁+x₂+…+x₂₀₀₃+x₂₀₀₄的值．

科目：czsx 来源： 题型：

在直角坐标系中，直线y=2x+4交x轴于A，交y轴于D
（1）以A为直角顶点作等腰直角△AMD，直接写出点M的坐标为

 

（2）以AD为边作正方形ABCD，连BD，P是线段BD上（不与B、D重合）的一点，在BD上截取PG=

10

，过G作GF⊥BD，交BC于F，连AP则AP与PF有怎样的数量关系和位置关系？并证明你的结论；
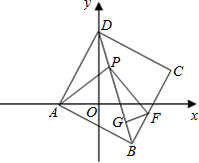
（3）在（2）中的正方形中，若∠PAG=45°，试判断线段PD、PG、BG之间有何关系，并证明你的结论．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

用配方法将二次函数y=x²-2x-3化为y=a（x-h）²+k的形式（其中h，k为常数），写出这个二次函数图象的顶点坐标和对称轴方程，并在直角坐标系中画出他的示意图．

科目：czsx 来源： 题型：

在直角坐标系中，描出A（-2，-3）、B（4，-3）、C（3，2）、D（-3，2）四点，并指出连接A、B、C、D、A后的图形是什么图形．并计算其面积．

科目：czsx 来源： 题型：

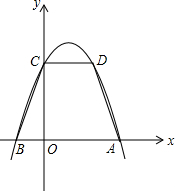
如图，在直角坐标系中，等腰梯形ABCD中，AB∥CD，AD=BC=

10

，AB=4，CD=2．抛物线y=ax²+bx+c经过A、B、C三点．
（1）求抛物线的函数表达式；
（2）点E是x轴上一点，且以E、A、D、C为顶点的四边形是平行四边形．若过B点的直线把这个四边形的面积分成相等的两部分，求该直线的函数表达式；
（3）P是抛物线对称轴上一点，连接PC、PA，是否存在△PAC是直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

在直角坐标系中，△ABC的位置如图所示．
（1）画出△ABC关于y轴对称的图形△A₁B₁C₁；
（2）写出点A₁，点B₁的坐标．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

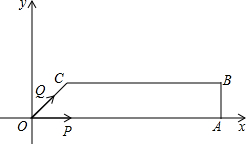
在直角坐标系中，O是原点，A、B、C三点的坐标分别为A（18，0），B（18，8），C（6，8），四边形OABC是梯形，点P、Q同时从原点出发，分别做匀速运动，其中点P沿OA向终点A运动，速度为每秒2个单位，点Q沿OC、CB向终点B运动，速度为每秒3个单位，当这两点有一点到达自己的终点则另一点也停止运动，设从出发起，运动了t秒．
①求直线OC的解析式．
②试写出点Q的坐标，并写出此时t的取值范围．
③从运动开始，梯形被直线PQ分割后的图形中是否存在平行四边形，若存在，求出t的值，若不存在，请说明理由．
④t为何值时，直线PQ把梯形OCBA分成面积为1：7的两部分？