科目:gzsx
来源:
题型:
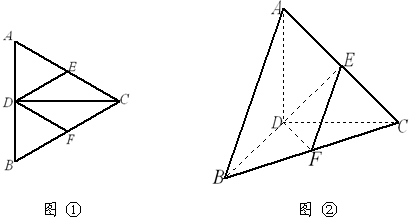
如图①,正三角形ABC边长2,CD为AB边上的高,E、F分别为AC、BC中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②
(1)判断翻折后直线AB与面DEF的位置关系,并说明理由
(2)求二面角B-AC-D的余弦值
(3)求点C到面DEF的距离
查看答案和解析>>
科目:gzsx
来源:2010-2011学年北京五中高三(上)期中数学试卷(理科)(解析版)
题型:解答题
如图①,正三角形ABC边长2,CD为AB边上的高,E、F分别为AC、BC中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②
(1)判断翻折后直线AB与面DEF的位置关系,并说明理由
(2)求二面角B-AC-D的余弦值
(3)求点C到面DEF的距离

查看答案和解析>>
科目:gzsx
来源:
题型:解答题
如图①,正三角形ABC边长2,CD为AB边上的高,E、F分别为AC、BC中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②
(1)判断翻折后直线AB与面DEF的位置关系,并说明理由
(2)求二面角B-AC-D的余弦值
(3)求点C到面DEF的距离

查看答案和解析>>
科目:gzsx
来源:
题型:013
已知正三角形ABC边长为2, PA⊥平面ABC, 且PA=1, 则点P到BC的距离是
[ ]
A.1 B.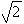 C.
C.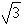 D.2
D.2
查看答案和解析>>
科目:gzsx
来源:
题型:
正三角形ABC边长为2,设
=2,
=3,则
•-2
-2
.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2009•长宁区二模)已知正三角形ABC边长为a,用这个三角形的高为边,作一个新的正三角形,再用这第二个正三角形的高为边作正三角形,…,这样无限继续下去,则所有正三角形的面积之和为
.
查看答案和解析>>
科目:gzsx
来源:
题型:

正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是
.
查看答案和解析>>
科目:gzsx
来源:
题型:
正三角形ABC边长为2,平面ABC外一点P,PA=PB=PC=
,则P到平面ABC的距离为( )
查看答案和解析>>
科目:gzsx
来源:2012-2013学年北京市海淀区八一中学高三(上)周练数学试卷(11)(理科)(解析版)
题型:填空题
查看答案和解析>>
科目:gzsx
来源:2009年上海市长宁区高考数学二模试卷(文科)(解析版)
题型:解答题
已知正三角形ABC边长为a,用这个三角形的高为边,作一个新的正三角形,再用这第二个正三角形的高为边作正三角形,…,这样无限继续下去,则所有正三角形的面积之和为 .
查看答案和解析>>
科目:gzsx
来源:不详
题型:填空题
正三角形ABC边长为2,设
=2,
=3,则
•______.
查看答案和解析>>
科目:gzsx
来源:
题型:044
已知正三角形
ABC边长为a,在平面内求一点P,使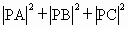 最小,并求出最小值.
最小,并求出最小值.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年重庆市重点中学六校联考高二(上)数学模拟试卷(3)(解析版)
题型:选择题
正三角形ABC边长为2,平面ABC外一点P,PA=PB=PC=

,则P到平面ABC的距离为( )
A.

B.

C.

D.
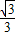
查看答案和解析>>
科目:gzsx
来源:
题型:013
正三角形ABC边长为1,BC边上的高是AD,若沿AD折成120°二面角后,A到BC的距离是
[
]

查看答案和解析>>
科目:gzsx
来源:2012-2013学年北京市东城区示范校高三(上)12月联考数学试卷(理科)(解析版)
题型:填空题
查看答案和解析>>
科目:gzsx
来源:
题型:
正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是
查看答案和解析>>
科目:gzsx
来源:
题型:填空题
正三角形ABC边长为2,设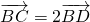 ,
,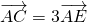 ,则
,则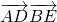 ________.
________.
查看答案和解析>>
科目:gzsx
来源:
题型:
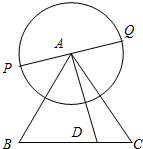
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
(1)若
=,求
||;
(2)求
•的最小值.
(3)判断
•+•的值是否会随点P的变化而变化,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
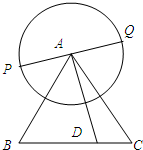
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
(1)若
=,求
||;
(2)求
•的最大值.
(3)判断
B•C-A•C的值是否会随点P的变化而变化,请说明理由.
查看答案和解析>>
科目:gzsx
来源:2014届江西省红色六校高三第一次联考理科数学试卷(解析版)
题型:填空题
查看答案和解析>>




 正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是
正三角形ABC边长为2,P,Q,R,分别是三边的中点,把△APQ,△BPR,△CQR分别沿PQ,PR,QR折起,使得A,B,C重合,M,N分别是△PQR,△BPR的中心,则在几何体中MN的长是 ,则P到平面ABC的距离为( )
,则P到平面ABC的距离为( )


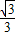

 如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径. 如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径.
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆,PQ为圆A的任意一条直径. =x
=x ,
, =y
=y ,x>0,y>0,且x+y=1,则
,x>0,y>0,且x+y=1,则  ·
·
 的最大值为_____________
的最大值为_____________