
科目:gzsx 来源:2012-2013学年黑龙江省高三上学期期末考试理科数学试卷(解析版) 题型:选择题
已知函数 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当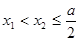 时,总有
时,总有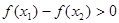 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.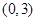 B.
B. C.
C. D.
D.
科目:gzsx 来源:2011-2012学年江苏省宿迁市沭阳县华冲中学高三(上)9月调研数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源:2010-2011学年江苏省连云港市新海高级中学高三(下)3月调研数学试卷(解析版) 题型:解答题
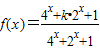
科目:gzsx 来源:安徽省蚌埠三中2011-2012学年高一12月月考数学试题 题型:044
已知函数![]() .
.
(1)证明:对于任意的a∈R,f(x)是R上的增函数;
(2)是否存在实数a使函数f(x)为奇函数?若存在,请求出a的值,若不存在,说明理由
.科目:gzsx 来源: 题型:解答题
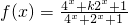
科目:gzsx 来源:江苏期末题 题型:解答题
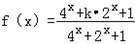
科目:gzsx 来源:2015届河南灵宝三中高一上学期质检数学试卷(解析版) 题型:解答题
(12分)已知函数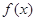 的定义域为
的定义域为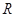 ,对于任意的
,对于任意的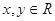 ,都有
,都有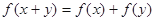 ,且当
,且当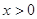 时,
时, .
.
(1)求证: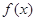 为奇函数; (2)求证:
为奇函数; (2)求证: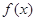 是
是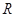 上的减函数;
上的减函数;
科目:gzsx 来源:2014届福建省三明市高一第一学期联合命题考试数学 题型:解答题
(本小题满分12分)
已知函数 的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有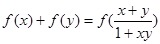 ,且当
,且当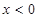 时,
时, .
.
(Ⅰ)验证函数 是否满足上述这些条件;
是否满足上述这些条件;
(Ⅱ)你发现这样的函数 还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.
还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.
科目:gzsx 来源:2015届山东省济宁市高一10月月考数学试卷(解析版) 题型:解答题
已知函数 的定义域为
的定义域为 ,对于任意的
,对于任意的 ,都有
,都有 ,且当
,且当 时,
时, ,若
,若 .
.
(1)求证: 为奇函数;
为奇函数;
(2)求证: 是
是 上的减函数;
上的减函数;
(3)求函数 在区间
在区间 上的值域.
上的值域.
科目:gzsx 来源: 题型:
(本题满分12分) 已知函数![]() 的定义域为
的定义域为![]() ,对于任意正数a、b,都有
,对于任意正数a、b,都有![]() ,其中p是常数,且
,其中p是常数,且![]() .
.![]() ,当
,当![]() 时,总有
时,总有![]() .
.
(1)求![]() (写成关于p的表达式);
(写成关于p的表达式);
(2)判断![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
科目:gzsx 来源:2014届江苏省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知函数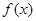 定义在
定义在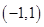 上,对于任意的
上,对于任意的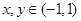 ,有
,有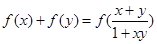 ,且当
,且当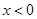 时,
时,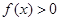 .
.
(1)验证函数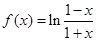 是否满足这些条件;
是否满足这些条件;
(2)若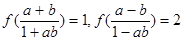 ,且
,且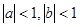 ,求
,求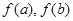 的值.
的值.
(3)若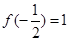 ,试解关于
,试解关于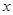 的方程
的方程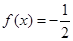 .
.
科目:gzsx 来源:2015届河南省许昌市五校高一上学期第一次联考数学试卷(解析版) 题型:解答题
已知函数 的定义域为
的定义域为 ,对于任意的
,对于任意的 ,都有
,都有 ,且当
,且当 时,
时, ,若
,若 .
.
(1)求证: 为奇函数;
为奇函数;
(2)求证: 是
是 上的减函数;
上的减函数;
(3)求函数 在区间
在区间 上的值域.
上的值域.
科目:gzsx 来源:2015届贵州省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 定义域为
定义域为 ,若对于任意的
,若对于任意的 ,都有
,都有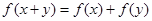 ,且
,且 时,有
时,有 .
.
(1)求证:  为奇函数;
为奇函数;
(2)求证:  在
在 上为单调递增函数;
上为单调递增函数;
(3)设 ,若
,若 <
< ,对所有
,对所有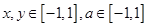 恒成立,求实数
恒成立,求实数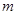 的取值范围.
的取值范围.
科目:gzsx 来源:2015届浙江省温州市高一第一次月考数学试卷(解析版) 题型:解答题
已知函数 定义域为
定义域为 ,若对于任意的
,若对于任意的 ,
,
 ,都有
,都有 ,且
,且 >0时,有
>0时,有 >0.
>0.
⑴证明:  为奇函数;
为奇函数;
⑵证明:  在
在 上为单调递增函数;
上为单调递增函数;
⑶设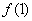 =1,若
=1,若 <
< ,对所有
,对所有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
本小题满分12分
已知函数![]() 定义域为
定义域为![]() ,若对于任意的
,若对于任意的![]() ,
,![]()
![]() ,都有
,都有![]() ,且
,且![]() >0时,有
>0时,有![]() >0.
>0.
⑴证明: ![]() 为奇函数;
为奇函数;
⑵证明: ![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
⑶设![]() =1,若
=1,若![]() <
<![]() ,对所有
,对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:gzsx 来源:吉林省东北师大附中2010届高三第一次摸底考试(理) 题型:解答题
已知函数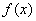 的定义域为
的定义域为 ,对于任意正数a、b,都有
,对于任意正数a、b,都有 ,其中p是常数,且
,其中p是常数,且 .
.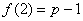 ,当
,当 时,总有
时,总有 .
.
(1)求 (写成关于p的表达式);
(写成关于p的表达式);
(2)判断 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)解关于 的不等式
的不等式
 .
.
科目:gzsx 来源: 题型:
| 2 |
| 3 |
| 4 |
| π |
| 3 |
| π |
| 3 |