精英家教网 >
试题搜索列表 >已知首项是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0
已知首项是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0答案解析
科目:gzsx
来源:
题型:
已知各项均为正数的两个数列{a
n}和{b
n}满足:
an+1=,n∈N
*.
(1)求证:当n≥2时,有
an≤成立;
(2)设
bn+1=,n∈N*,求证:数列
{()2}是等差数列;
(3)设b
n+1=a
nb
n,n∈N*,试问{a
n}可能为等比数列吗?若可能,请求出公比的值,若不可能,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=
,n∈N
﹡,
(Ⅰ)设b
n+1=1+
,n∈N
﹡,求证:
(1)
=
;
(2)数列{
()2}是等差数列,并求出其公差;
(Ⅱ)设
bn+1=•,n∈N
﹡,且{a
n}是等比数列,求a
1和b
1的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•江苏)已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=
,n∈N
*,
(1)设b
n+1=1+
,n∈N*,,求证:数列
{() 2}是等差数列;
(2)设b
n+1=
•
,n∈N*,且{a
n}是等比数列,求a
1和b
1的值.
查看答案和解析>>
科目:gzsx
来源:2012年普通高等学校招生全国统一考试江苏卷数学
题型:044
查看答案和解析>>
科目:gzsx
来源:2013年高考数学压轴大题训练:等差、等比数列的判断及其基本量的求解问题(解析版)
题型:解答题
已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=

,n∈N
*,
(1)设b
n+1=1+
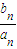
,n∈N*,,求证:数列
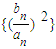
是等差数列;
(2)设b
n+1=

•

,n∈N*,且{a
n}是等比数列,求a
1和b
1的值.
查看答案和解析>>
科目:gzsx
来源:高考真题
题型:解答题
已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=

,n∈N*,
(1)设b
n+1=1+
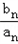
,n∈N*,求证:数列

是等差数列;
(2)设b
n+1=

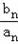
,n∈N*,且{a
n}是等比数列,求a
1和b
1的值。
查看答案和解析>>
科目:gzsx
来源:2012-2013学年浙江省绍兴一中高三(上)10月段考数学试卷(理科)(解析版)
题型:解答题
已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=

,n∈N
﹡,
(Ⅰ)设b
n+1=1+

,n∈N
﹡,求证:
(1)

=

;
(2)数列{

}是等差数列,并求出其公差;
(Ⅱ)设

,n∈N
﹡,且{a
n}是等比数列,求a
1和b
1的值.
查看答案和解析>>
科目:gzsx
来源:2012年江苏省高考数学试卷(解析版)
题型:解答题
已知各项均为正数的两个数列{a
n}和{b
n}满足:a
n+1=

,n∈N
*,
(1)设b
n+1=1+

,n∈N*,,求证:数列

是等差数列;
(2)设b
n+1=

•

,n∈N*,且{a
n}是等比数列,求a
1和b
1的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知各项均为正数的两个数列{a
n},{b
n},由下表给出:
| n |
1 |
2 |
3 |
4 |
5 |
| an |
1 |
5 |
3 |
1 |
2 |
| bn |
1 |
6 |
2 |
x |
y |
定义数列{c
n}:
c1=0,cn= | | bn,cn-1>an | | cn-1-an+bn,cn-1≤an |
| |
(n=2,3,4,5),并规定数列{a
n},{b
n}的“并和”为S
ab=a
1+a
2+…+a
5+c
5,若S
ab=15,则y的最小值为
3
3
.
查看答案和解析>>
科目:gzsx
来源:2013年江苏省南通市高考学科基地数学模拟试卷(十)(解析版)
题型:填空题
已知各项均为正数的两个数列{a
n},{b
n},由下表给出:
定义数列{c
n}:

,并规定数列{a
n},{b
n}的“并和”为S
ab=a
1+a
2+…+a
5+c
5,若S
ab=15,则y的最小值为
.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江苏省南京市高三(上)期中数学试卷(文科)(解析版)
题型:填空题
已知各项均为正数的两个数列{a
n},{b
n},由下表给出:
定义数列{c
n}:

,并规定数列{a
n},{b
n}的“并和”为S
ab=a
1+a
2+…+a
5+c
5,若S
ab=15,则y的最小值为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•哈尔滨一模)已知首项是1的等比数列{a
n}的前n项的和为S
n,a
2a
6-8a
4=0,则
=( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知首项是1的等比数列{a
n}的前n项和为S
n,a
2a
6=64,则
的值是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•静安区一模)已知椭圆
+=1的两个焦点为F
1(-c,0)、F
2(c,0),c
2是a
2与b
2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
.
(1)求椭圆的方程;
(2)过点A作直线交椭圆于另一点M,求|AM|长度的最大值;
(3)已知定点E(-1,0),直线y=kx+t与椭圆交于C、D相异两点.证明:对任意的t>0,都存在实数k,使得以线段CD为直径的圆过E点.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•静安区一模)已知椭圆
+=1的两个焦点为F
1(-c,0)、F
2(c,0),c
2是a
2与b
2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
.
(1)求椭圆的方程;
(2)点P是椭圆上一动点,定点A
1(0,2),求△F
1PA
1面积的最大值;
(3)已知定点E(-1,0),直线y=kx+t与椭圆交于C、D相异两点.证明:对任意的t>0,都存在实数k,使得以线段CD为直径的圆过E点.
查看答案和解析>>
科目:gzsx
来源:静安区一模
题型:解答题
已知椭圆
+=1的两个焦点为F
1(-c,0)、F
2(c,0),c
2是a
2与b
2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
.
(1)求椭圆的方程;
(2)点P是椭圆上一动点,定点A
1(0,2),求△F
1PA
1面积的最大值;
(3)已知定点E(-1,0),直线y=kx+t与椭圆交于C、D相异两点.证明:对任意的t>0,都存在实数k,使得以线段CD为直径的圆过E点.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•深圳二模)已知首项为1的数列{a
n}满足:对任意正整数n,都有:
a1•2-1+a2•2-1+a3•2-1+…+an•2-1=(n2-2n+3)•2n+c,其中c是常数.
(Ⅰ)求实数c的值;
(Ⅱ)求数列{a
n}的通项公式;
(Ⅲ)设数列
{•(-)-1}的前n项和为S
n,求证:S
2n-1>S
2m,其中m,n∈N
*.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知由正数组成的两个数列{a
n},{b
n},如果a
n,a
n+1是关于x的方程x
2-2b
n2x+a
nb
nb
n+1=0的两根.
(1)求证:{b
n}为等差数列;
(2)已知a
1=2,a
2=6,分别求数列{a
n},{b
n}的通项公式;
(3)求数
{}的前n项和S.
查看答案和解析>>
科目:gzsx
来源:2013年上海市杨浦区高考数学一模试卷(文科)(解析版)
题型:解答题
已知椭圆C:

+
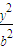
=1的两个焦点分别是F
1(-1,0)、F
2(1,0),且焦距是椭圆C上一点p到两焦点F
1,F
2距离的等差中项.
(1)求椭圆C的方程;
(2)设经过点F
2的直线交椭圆C于M,N两点,线段MN的垂直平分线交y轴于点Q(x
,y
),求y
的取值范围.
查看答案和解析>>

 ,n∈N+.
,n∈N+.![]() ,n∈N+,求证:数列{(
,n∈N+,求证:数列{(![]() )2}是等差数列;
)2}是等差数列;![]() ·
·![]() ,n∈N+,且{an}是等比数列,求a1和b1的值.
,n∈N+,且{an}是等比数列,求a1和b1的值. ,n∈N*,
,n∈N*,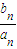 ,n∈N*,,求证:数列
,n∈N*,,求证:数列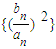 是等差数列;
是等差数列; •
• ,n∈N*,且{an}是等比数列,求a1和b1的值.
,n∈N*,且{an}是等比数列,求a1和b1的值. ,n∈N*,
,n∈N*,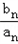 ,n∈N*,求证:数列
,n∈N*,求证:数列 是等差数列;
是等差数列;
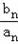 ,n∈N*,且{an}是等比数列,求a1和b1的值。
,n∈N*,且{an}是等比数列,求a1和b1的值。 ,n∈N﹡,
,n∈N﹡, ,n∈N﹡,求证:
,n∈N﹡,求证: =
= ;
; }是等差数列,并求出其公差;
}是等差数列,并求出其公差; ,n∈N﹡,且{an}是等比数列,求a1和b1的值.
,n∈N﹡,且{an}是等比数列,求a1和b1的值. ,n∈N*,
,n∈N*, ,n∈N*,,求证:数列
,n∈N*,,求证:数列 是等差数列;
是等差数列; •
• ,n∈N*,且{an}是等比数列,求a1和b1的值.
,n∈N*,且{an}是等比数列,求a1和b1的值. ,并规定数列{an},{bn}的“并和”为Sab=a1+a2+…+a5+c5,若Sab=15,则y的最小值为 .
,并规定数列{an},{bn}的“并和”为Sab=a1+a2+…+a5+c5,若Sab=15,则y的最小值为 .  ,并规定数列{an},{bn}的“并和”为Sab=a1+a2+…+a5+c5,若Sab=15,则y的最小值为 .
,并规定数列{an},{bn}的“并和”为Sab=a1+a2+…+a5+c5,若Sab=15,则y的最小值为 .  +
+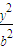 =1的两个焦点分别是F1(-1,0)、F2(1,0),且焦距是椭圆C上一点p到两焦点F1,F2距离的等差中项.
=1的两个焦点分别是F1(-1,0)、F2(1,0),且焦距是椭圆C上一点p到两焦点F1,F2距离的等差中项.