
科目:czsx 来源: 题型:
 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.科目:czsx 来源: 题型:
| 1 |
| 4 |
| 1 |
| 3 |
科目:czsx 来源: 题型:解答题
 如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,
如图,△ABC是等边三角形,BE⊥AC于E,点F、G在BE上(BF<BG),连接AF,CG,CG2=GF•GB,科目:czsx 来源: 题型:
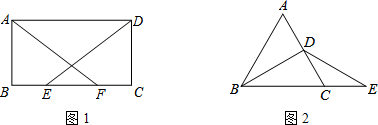
.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设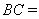
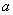 ,
,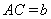 ,
,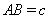 .
.
特例探索
(1)如图1,当∠ =45°,
=45°, 时,
时,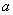 = ,
= , ;
;
如图2,当∠ =30°,
=30°, 时,
时, 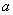 = ,
= , ;
;
归纳证明
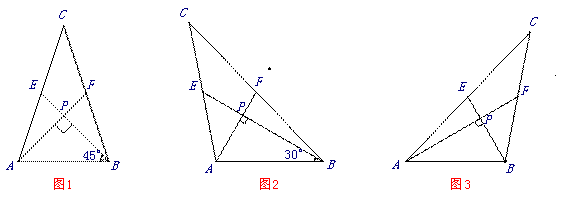
(2)请你观察(1)中的计算结果,猜想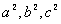 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
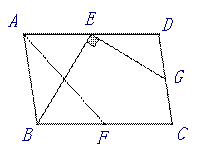
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD= 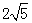 ,AB=3.
,AB=3.
求AF的长.
科目:czsx 来源: 题型:
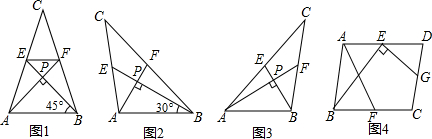
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c= 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;

归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD= ,AB=3.求AF的长.
,AB=3.求AF的长.

科目:czsx 来源:2015年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=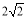 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;

归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=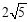 ,AB=3.求AF的长.
,AB=3.求AF的长.

科目:czsx 来源:2016届浙江省台州市九年级上学期第三次月考数学试卷(解析版) 题型:解答题
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
 ,
, ,
, .
.
特例探索
(1)如图1,当∠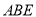 =45°,
=45°,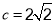 时,
时, = ,
= , ;
;
如图2,当∠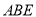 =30°,
=30°, 时,
时,  = ,
= , ;
;
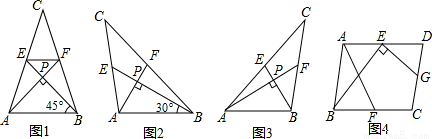
归纳证明
(2)请你观察(1)中的计算结果,猜想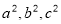 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=  ,AB=3.求AF的长.
,AB=3.求AF的长.
科目:czsx 来源:2016届福建省泉州市泉港区九年级12月教学质量检测数学试卷(解析版) 题型:解答题
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设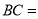
 ,
, ,
, .
.

特例探索
(1)如图1,当∠ =45°,
=45°,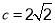 时,
时, = ,
= ,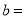 ;
;
如图2,当∠ =30°,
=30°, 时,
时,  = ,
= ,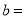 ;
;
归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,
三者之间的关系,用等式表示出来,
并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD= ,AB=6.
,AB=6.
求AF的长.
科目:czsx 来源:2015年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
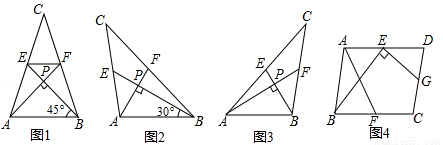
特例探索
(1)如图1,当∠ABE=45°,c= 时,a= ,b= .
时,a= ,b= .
如图2,当∠ABE=30°,c=4时,a= ,b= .
归纳证明
(2)请你观察(1)中的计算结果,猜想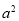 ,
,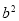 ,
, 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=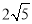 ,AB=3,求AF的长.
,AB=3,求AF的长.
科目:czsx 来源:2016届河南省商丘市中考四模数学试卷(解析版) 题型:解答题
我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
特例探索

(1)如图1,当∠ABE=45°,c=2 时,a=_____________,b=_____________.
时,a=_____________,b=_____________.
如图2,当∠ABE=30°,c=4时,a=_____________,b=_____________.
归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
(3)如图4,在▱ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3,求AF的长.
,AB=3,求AF的长.
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2016年初中毕业升学考试(辽宁沈阳卷)数学(解析版) 题型:解答题
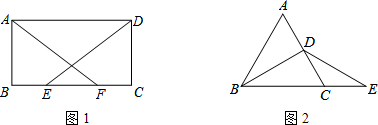
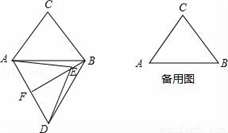
在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
科目:czsx 来源: 题型:解答题
